Question Number 2205 by prakash jain last updated on 08/Nov/15
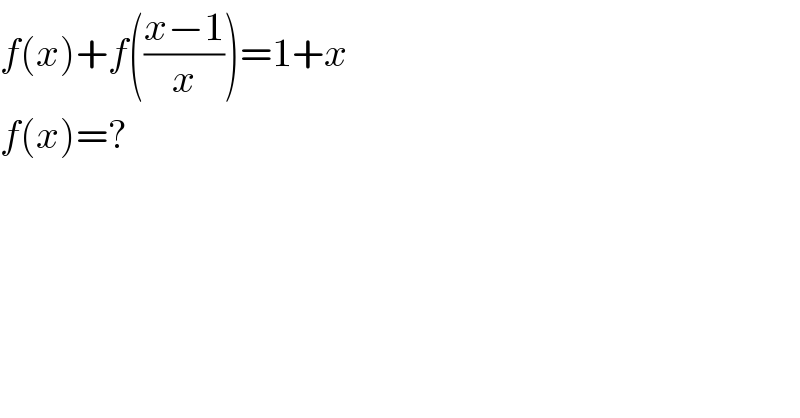
$${f}\left({x}\right)+{f}\left(\frac{{x}−\mathrm{1}}{{x}}\right)=\mathrm{1}+{x} \\ $$$${f}\left({x}\right)=? \\ $$
Commented by Yozzi last updated on 08/Nov/15
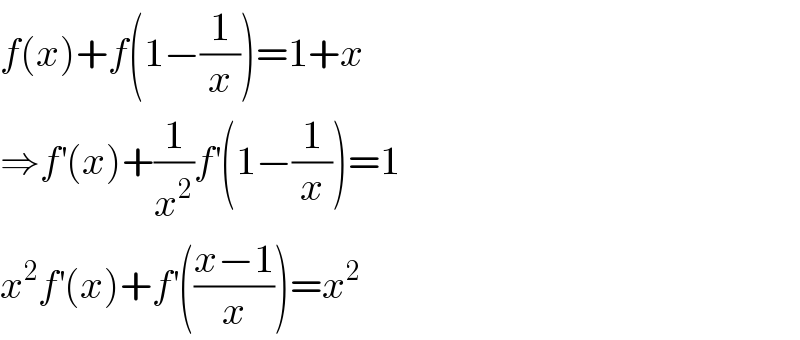
$${f}\left({x}\right)+{f}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)=\mathrm{1}+{x} \\ $$$$\Rightarrow{f}^{'} \left({x}\right)+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{f}^{'} \left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)=\mathrm{1} \\ $$$${x}^{\mathrm{2}} {f}^{'} \left({x}\right)+{f}^{'} \left(\frac{{x}−\mathrm{1}}{{x}}\right)={x}^{\mathrm{2}} \\ $$
Answered by Rasheed Soomro last updated on 10/Nov/15
![f(x)+f(((x−1)/x))=1+x f(x)=1+x−f(((x−1)/x))...............................(1) f(((x−1)/x))=1+((x−1)/x)−f(((((x−1)/x)−1)/((x−1)/x))) [Replacing x by ((x−1)/x) in (1)] =1+((x−1)/x)−f(((−1)/(x−1)))......................(2) f(((−1)/(x−1)))=1+((−1)/(x−1))−f(((((−1)/(x−1))−1)/((−1)/(x−1)))) [Replacing x by ((−1)/(x−1)) in (1)] =1−(1/(x−1))−f(x)...........................(3) −−−−−−−−−−−−−−−−−− Replacing f(((x−1)/x)) by rhs of (2) and f(((−1)/(x−1))) by rhs of (3) and f(x) by rhs of (1) in (1) f(x)=1+x−f(((x−1)/x)) f(x)=1+x−[1+((x−1)/x)−f(((−1)/(x−1)))] f(x)=x−((x−1)/x)+f(((−1)/(x−1)))] =x−((x−1)/x)+1−(1/(x−1))−f(x) 2f(x)=x−((x−1)/x)+1−(1/(x−1)) f(x)=(1/2)(x−((x−1)/x)−(1/(x−1))+1) −−−−−−−−−−−−−−−−−−−−−−−−− VERIFICATION: f(x)=(1/2)(x−((x−1)/x)−(1/(x−1))+1) f(((x−1)/x))=(1/2)(((x−1)/x)−((((x−1)/x)−1)/((x−1)/x))−(1/(((x−1)/x)−1))+1) =(1/2)(((x−1)/x)+(1/(x−1))+x+1) f(x)+f(((x−1)/x))=(1/2)(x−((x−1)/x)^(×) −(1/(x−1))^(×) +1+((x−1)/x)^(×) +(1/(x−1))^(×) +x+1) =(1/2)(2x+2) =x+1](https://www.tinkutara.com/question/Q2239.png)
$${f}\left({x}\right)+{f}\left(\frac{{x}−\mathrm{1}}{{x}}\right)=\mathrm{1}+{x} \\ $$$${f}\left({x}\right)=\mathrm{1}+{x}−{f}\left(\frac{{x}−\mathrm{1}}{{x}}\right)………………………….\left(\mathrm{1}\right) \\ $$$${f}\left(\frac{{x}−\mathrm{1}}{{x}}\right)=\mathrm{1}+\frac{{x}−\mathrm{1}}{{x}}−{f}\left(\frac{\frac{{x}−\mathrm{1}}{{x}}−\mathrm{1}}{\frac{{x}−\mathrm{1}}{{x}}}\right)\:\:\:\:\left[{Replacing}\:{x}\:{by}\:\frac{{x}−\mathrm{1}}{{x}}\:{in}\:\left(\mathrm{1}\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{1}+\frac{{x}−\mathrm{1}}{{x}}−{f}\left(\frac{−\mathrm{1}}{{x}−\mathrm{1}}\right)………………….\left(\mathrm{2}\right) \\ $$$${f}\left(\frac{−\mathrm{1}}{{x}−\mathrm{1}}\right)=\mathrm{1}+\frac{−\mathrm{1}}{{x}−\mathrm{1}}−{f}\left(\frac{\frac{−\mathrm{1}}{{x}−\mathrm{1}}−\mathrm{1}}{\frac{−\mathrm{1}}{{x}−\mathrm{1}}}\right)\:\:\:\left[{Replacing}\:{x}\:{by}\:\frac{−\mathrm{1}}{{x}−\mathrm{1}}\:{in}\:\left(\mathrm{1}\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{1}−\frac{\mathrm{1}}{{x}−\mathrm{1}}−{f}\left({x}\right)………………………\left(\mathrm{3}\right) \\ $$$$−−−−−−−−−−−−−−−−−− \\ $$$${Replacing}\:{f}\left(\frac{{x}−\mathrm{1}}{{x}}\right)\:{by}\:\:{rhs}\:{of}\:\left(\mathrm{2}\right)\:\:\:{and}\:\:{f}\left(\frac{−\mathrm{1}}{{x}−\mathrm{1}}\right)\:\:{by}\:{rhs}\:{of}\:\:\left(\mathrm{3}\right) \\ $$$${and}\:\:{f}\left({x}\right)\:{by}\:{rhs}\:{of}\:\:\left(\mathrm{1}\right)\:{in}\:\left(\mathrm{1}\right) \\ $$$${f}\left({x}\right)=\mathrm{1}+{x}−{f}\left(\frac{{x}−\mathrm{1}}{{x}}\right) \\ $$$${f}\left({x}\right)=\mathrm{1}+{x}−\left[\mathrm{1}+\frac{{x}−\mathrm{1}}{{x}}−{f}\left(\frac{−\mathrm{1}}{{x}−\mathrm{1}}\right)\right] \\ $$$$\left.{f}\left({x}\right)={x}−\frac{{x}−\mathrm{1}}{{x}}+{f}\left(\frac{−\mathrm{1}}{{x}−\mathrm{1}}\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:={x}−\frac{{x}−\mathrm{1}}{{x}}+\mathrm{1}−\frac{\mathrm{1}}{{x}−\mathrm{1}}−{f}\left({x}\right) \\ $$$$\mathrm{2}{f}\left({x}\right)={x}−\frac{{x}−\mathrm{1}}{{x}}+\mathrm{1}−\frac{\mathrm{1}}{{x}−\mathrm{1}} \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left({x}−\frac{{x}−\mathrm{1}}{{x}}−\frac{\mathrm{1}}{{x}−\mathrm{1}}+\mathrm{1}\right) \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$$\mathcal{VERIFICATION}: \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left({x}−\frac{{x}−\mathrm{1}}{{x}}−\frac{\mathrm{1}}{{x}−\mathrm{1}}+\mathrm{1}\right) \\ $$$${f}\left(\frac{{x}−\mathrm{1}}{{x}}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{x}−\mathrm{1}}{{x}}−\frac{\frac{{x}−\mathrm{1}}{{x}}−\mathrm{1}}{\frac{{x}−\mathrm{1}}{{x}}}−\frac{\mathrm{1}}{\frac{{x}−\mathrm{1}}{{x}}−\mathrm{1}}+\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{x}−\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{x}−\mathrm{1}}+{x}+\mathrm{1}\right) \\ $$$${f}\left({x}\right)+{f}\left(\frac{{x}−\mathrm{1}}{{x}}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left({x}−\overset{×} {\frac{{x}−\mathrm{1}}{{x}}}−\overset{×} {\frac{\mathrm{1}}{{x}−\mathrm{1}}}+\mathrm{1}+\overset{×} {\frac{{x}−\mathrm{1}}{{x}}}+\overset{×} {\frac{\mathrm{1}}{{x}−\mathrm{1}}}+{x}+\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{x}+\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={x}+\mathrm{1} \\ $$
Commented by Rasheed Soomro last updated on 11/Nov/15

$${f}\left({x}\right)\:{involves}\:{f}\left(\frac{{x}−\mathrm{1}}{{x}}\right),\:\:{f}\left(\frac{{x}−\mathrm{1}}{{x}}\right)\:{involves}\:{f}\left(\frac{−\mathrm{1}}{{x}−\mathrm{1}}\right) \\ $$$${and}\:{f}\left(\frac{−\mathrm{1}}{{x}−\mathrm{1}}\right)\:{involves}\:{again}\:{f}\left({x}\right).\:{This}\:{is}\:{cyclic}.{At}\:{last} \\ $$$${we}\:{have}\:{an}\:{equation}\:{which}\:{involves}\:{only}\:{f}\left({x}\right)\:{which} \\ $$$${gives}\:{definition}\:{of}\:{f}\left({x}\right).{I}\:{think}\:{this}\:{cyclic}\:\:{type}\: \\ $$$${functional}\:{equation}\:{shows}\:{a}\:{categary}\:{of}\:{functional} \\ $$$${equations}. \\ $$$$\:\:\:\:{We}\:{can}\:{also}\:{talk}\:{of}\:\:{order}\:{of}\:{such}\:{equations}. \\ $$
