Question Number 4817 by 123456 last updated on 15/Mar/16
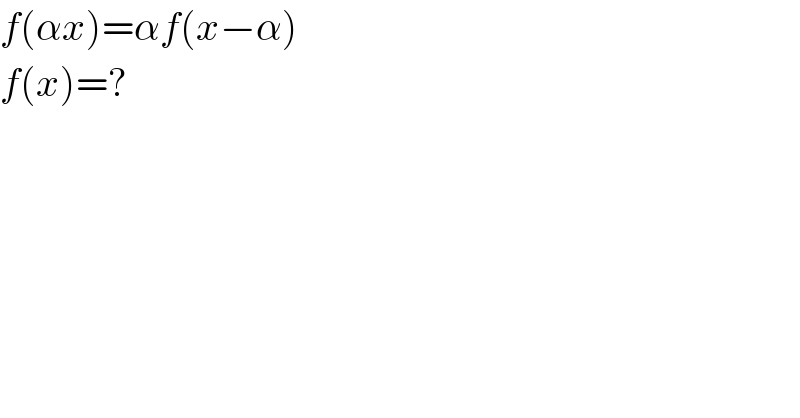
$${f}\left(\alpha{x}\right)=\alpha{f}\left({x}−\alpha\right) \\ $$$${f}\left({x}\right)=? \\ $$
Commented by prakash jain last updated on 15/Mar/16
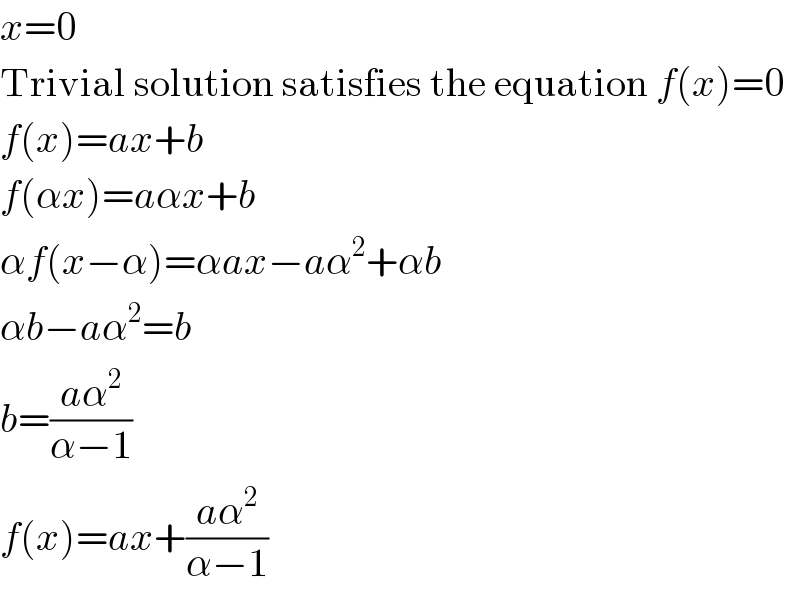
$${x}=\mathrm{0} \\ $$$$\mathrm{Trivial}\:\mathrm{solution}\:\mathrm{satisfies}\:\mathrm{the}\:\mathrm{equation}\:{f}\left({x}\right)=\mathrm{0} \\ $$$${f}\left({x}\right)={ax}+{b} \\ $$$${f}\left(\alpha{x}\right)={a}\alpha{x}+{b} \\ $$$$\alpha{f}\left({x}−\alpha\right)=\alpha{ax}−{a}\alpha^{\mathrm{2}} +\alpha{b} \\ $$$$\alpha{b}−{a}\alpha^{\mathrm{2}} ={b} \\ $$$${b}=\frac{{a}\alpha^{\mathrm{2}} }{\alpha−\mathrm{1}} \\ $$$${f}\left({x}\right)={ax}+\frac{{a}\alpha^{\mathrm{2}} }{\alpha−\mathrm{1}} \\ $$
