Menu Close

f-x-g-x-0-f-x-g-x-0-f-x-g-x-

Tinku Tara 0 Comments
Pin




Question Number 1930 by Rasheed Soomro last updated on 24/Oct/15
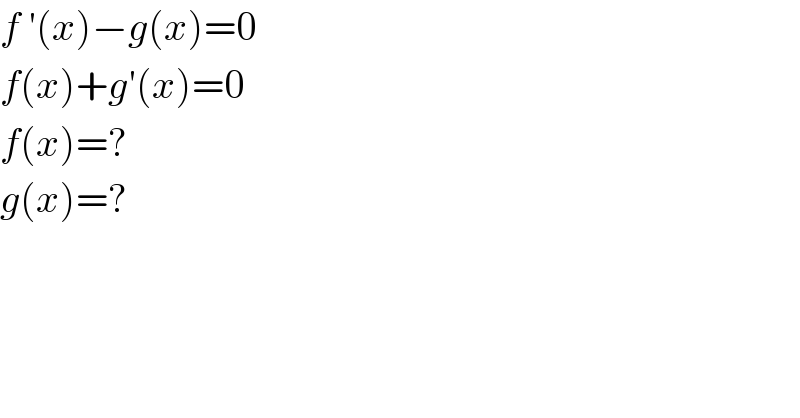
f ′(x)−g(x)=0 f(x)+g′(x)=0 f(x)=? g(x)=?
$${f}\:'\left({x}\right)−{g}\left({x}\right)=\mathrm{0} \\ $$$${f}\left({x}\right)+{g}'\left({x}\right)=\mathrm{0} \\ $$$${f}\left({x}\right)=? \\ $$$${g}\left({x}\right)=? \\ $$
Answered by prakash jain last updated on 24/Oct/15
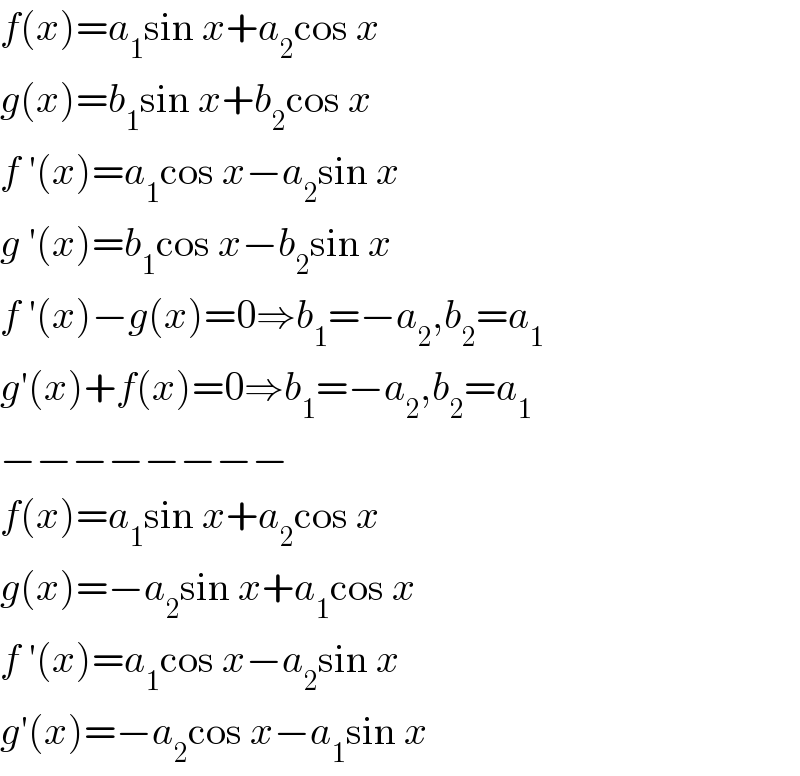
f(x)=a_1 sin x+a_2 cos x g(x)=b_1 sin x+b_2 cos x f ′(x)=a_1 cos x−a_2 sin x g ′(x)=b_1 cos x−b_2 sin x f ′(x)−g(x)=0⇒b_1 =−a_2 ,b_2 =a_1 g′(x)+f(x)=0⇒b_1 =−a_2 ,b_2 =a_1 −−−−−−−− f(x)=a_1 sin x+a_2 cos x g(x)=−a_2 sin x+a_1 cos x f ′(x)=a_1 cos x−a_2 sin x g′(x)=−a_2 cos x−a_1 sin x
$${f}\left({x}\right)={a}_{\mathrm{1}} \mathrm{sin}\:{x}+{a}_{\mathrm{2}} \mathrm{cos}\:{x} \\ $$$${g}\left({x}\right)={b}_{\mathrm{1}} \mathrm{sin}\:{x}+{b}_{\mathrm{2}} \mathrm{cos}\:{x} \\ $$$${f}\:'\left({x}\right)={a}_{\mathrm{1}} \mathrm{cos}\:{x}−{a}_{\mathrm{2}} \mathrm{sin}\:{x} \\ $$$${g}\:'\left({x}\right)={b}_{\mathrm{1}} \mathrm{cos}\:{x}−{b}_{\mathrm{2}} \mathrm{sin}\:{x} \\ $$$${f}\:'\left({x}\right)−{g}\left({x}\right)=\mathrm{0}\Rightarrow{b}_{\mathrm{1}} =−{a}_{\mathrm{2}} ,{b}_{\mathrm{2}} ={a}_{\mathrm{1}} \\ $$$${g}'\left({x}\right)+{f}\left({x}\right)=\mathrm{0}\Rightarrow{b}_{\mathrm{1}} =−{a}_{\mathrm{2}} ,{b}_{\mathrm{2}} ={a}_{\mathrm{1}} \\ $$$$−−−−−−−− \\ $$$${f}\left({x}\right)={a}_{\mathrm{1}} \mathrm{sin}\:{x}+{a}_{\mathrm{2}} \mathrm{cos}\:{x} \\ $$$${g}\left({x}\right)=−{a}_{\mathrm{2}} \mathrm{sin}\:{x}+{a}_{\mathrm{1}} \mathrm{cos}\:{x} \\ $$$${f}\:'\left({x}\right)={a}_{\mathrm{1}} \mathrm{cos}\:{x}−{a}_{\mathrm{2}} \mathrm{sin}\:{x} \\ $$$${g}'\left({x}\right)=−{a}_{\mathrm{2}} \mathrm{cos}\:{x}−{a}_{\mathrm{1}} \mathrm{sin}\:{x} \\ $$
Answered by 123456 last updated on 24/Oct/15
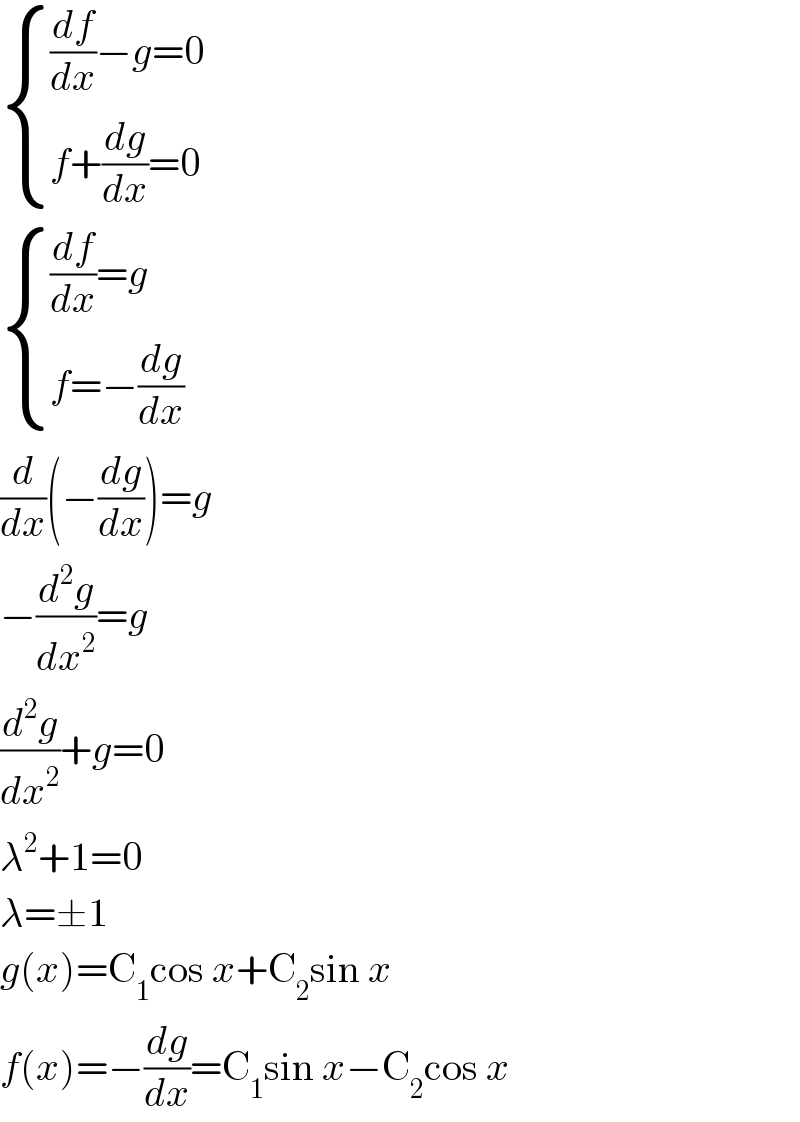
{ (((df/dx)−g=0)),((f+(dg/dx)=0)) :} { (((df/dx)=g)),((f=−(dg/dx))) :} (d/dx)(−(dg/dx))=g −(d^2 g/dx^2 )=g (d^2 g/dx^2 )+g=0 λ^2 +1=0 λ=±1 g(x)=C_1 cos x+C_2 sin x f(x)=−(dg/dx)=C_1 sin x−C_2 cos x
$$\begin{cases}{\frac{{df}}{{dx}}−{g}=\mathrm{0}}\\{{f}+\frac{{dg}}{{dx}}=\mathrm{0}}\end{cases} \\ $$$$\begin{cases}{\frac{{df}}{{dx}}={g}}\\{{f}=−\frac{{dg}}{{dx}}}\end{cases} \\ $$$$\frac{{d}}{{dx}}\left(−\frac{{dg}}{{dx}}\right)={g} \\ $$$$−\frac{{d}^{\mathrm{2}} {g}}{{dx}^{\mathrm{2}} }={g} \\ $$$$\frac{{d}^{\mathrm{2}} {g}}{{dx}^{\mathrm{2}} }+{g}=\mathrm{0} \\ $$$$\lambda^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\lambda=\pm\mathrm{1} \\ $$$${g}\left({x}\right)=\mathrm{C}_{\mathrm{1}} \mathrm{cos}\:{x}+\mathrm{C}_{\mathrm{2}} \mathrm{sin}\:{x} \\ $$$${f}\left({x}\right)=−\frac{{dg}}{{dx}}=\mathrm{C}_{\mathrm{1}} \mathrm{sin}\:{x}−\mathrm{C}_{\mathrm{2}} \mathrm{cos}\:{x} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *