Question Number 10242 by FilupSmith last updated on 31/Jan/17
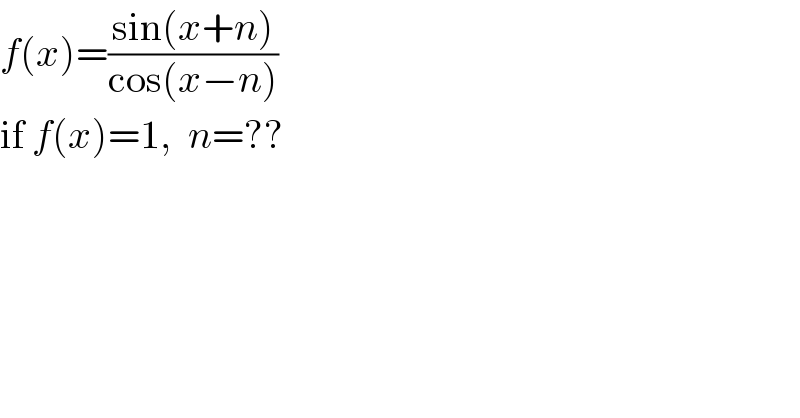
$${f}\left({x}\right)=\frac{\mathrm{sin}\left({x}+{n}\right)}{\mathrm{cos}\left({x}−{n}\right)} \\ $$$$\mathrm{if}\:{f}\left({x}\right)=\mathrm{1},\:\:{n}=?? \\ $$
Commented by arge last updated on 03/Feb/17

$${ojo}\:{con}\:{las}\:{identidades}\:{y}\:{derivadas}.\:{Salu}\mathrm{2}. \\ $$
Answered by mrW1 last updated on 31/Jan/17
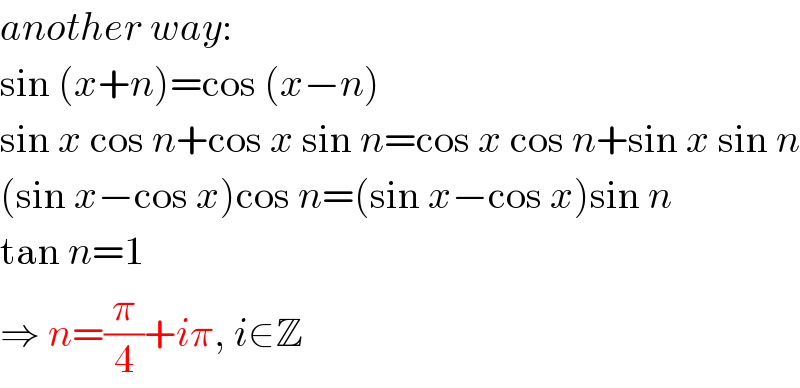
$${another}\:{way}: \\ $$$$\mathrm{sin}\:\left({x}+{n}\right)=\mathrm{cos}\:\left({x}−{n}\right) \\ $$$$\mathrm{sin}\:{x}\:\mathrm{cos}\:{n}+\mathrm{cos}\:{x}\:\mathrm{sin}\:{n}=\mathrm{cos}\:{x}\:\mathrm{cos}\:{n}+\mathrm{sin}\:{x}\:\mathrm{sin}\:{n} \\ $$$$\left(\mathrm{sin}\:{x}−\mathrm{cos}\:{x}\right)\mathrm{cos}\:{n}=\left(\mathrm{sin}\:{x}−\mathrm{cos}\:{x}\right)\mathrm{sin}\:{n} \\ $$$$\mathrm{tan}\:{n}=\mathrm{1} \\ $$$$\Rightarrow\:{n}=\frac{\pi}{\mathrm{4}}+{i}\pi,\:{i}\in\mathbb{Z} \\ $$
Answered by arge last updated on 03/Feb/17
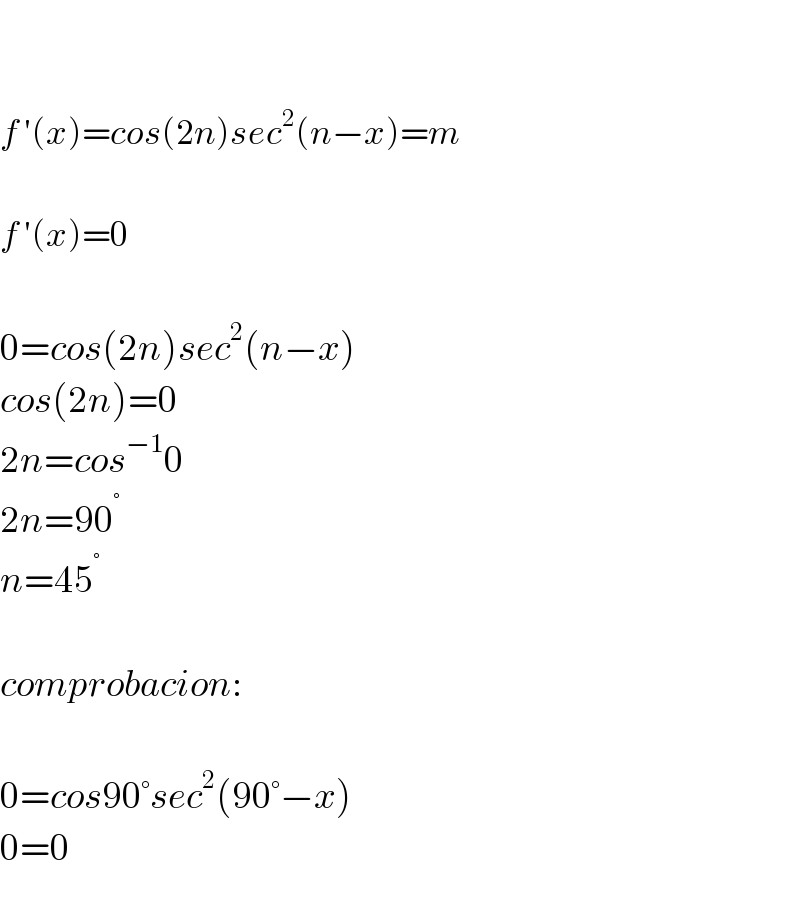
$$ \\ $$$$ \\ $$$${f}\:'\left({x}\right)={cos}\left(\mathrm{2}{n}\right){sec}^{\mathrm{2}} \left({n}−{x}\right)={m} \\ $$$$ \\ $$$${f}\:'\left({x}\right)=\mathrm{0} \\ $$$$ \\ $$$$\mathrm{0}={cos}\left(\mathrm{2}{n}\right){sec}^{\mathrm{2}} \left({n}−{x}\right) \\ $$$${cos}\left(\mathrm{2}{n}\right)=\mathrm{0} \\ $$$$\mathrm{2}{n}={cos}^{−\mathrm{1}} \mathrm{0} \\ $$$$\mathrm{2}{n}=\mathrm{90}^{°} \\ $$$${n}=\mathrm{45}^{°} \\ $$$$ \\ $$$${comprobacion}: \\ $$$$ \\ $$$$\mathrm{0}={cos}\mathrm{90}°{sec}^{\mathrm{2}} \left(\mathrm{90}°−{x}\right) \\ $$$$\mathrm{0}=\mathrm{0} \\ $$
