Menu Close

f-x-x-5-x-2-x-6-find-f-x-

Tinku Tara 0 Comments
Pin




Question Number 74959 by aliesam last updated on 04/Dec/19
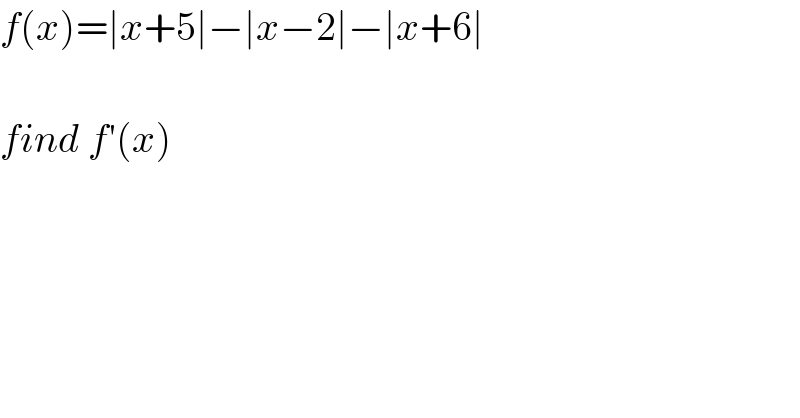
f(x)=∣x+5∣−∣x−2∣−∣x+6∣ find f′(x)
$${f}\left({x}\right)=\mid{x}+\mathrm{5}\mid−\mid{x}−\mathrm{2}\mid−\mid{x}+\mathrm{6}\mid \\ $$$$ \\ $$$${find}\:{f}'\left({x}\right) \\ $$
Commented by mathmax by abdo last updated on 04/Dec/19
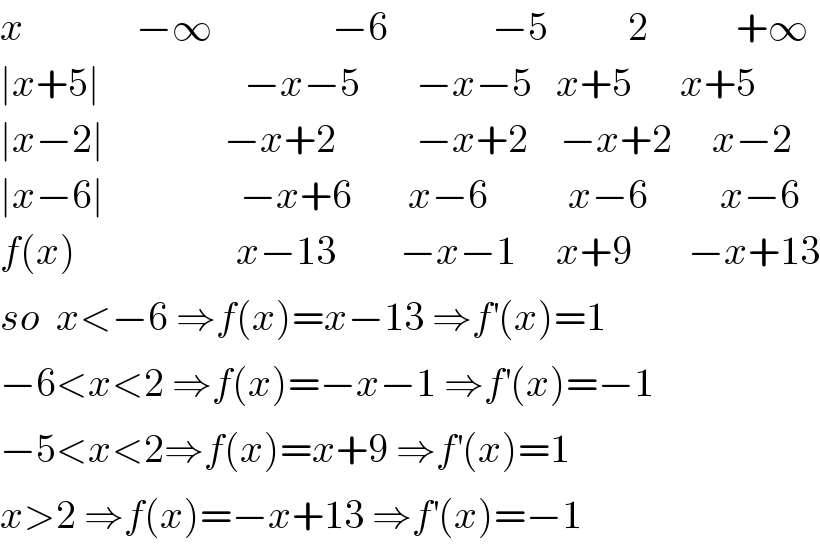
x −∞ −6 −5 2 +∞ ∣x+5∣ −x−5 −x−5 x+5 x+5 ∣x−2∣ −x+2 −x+2 −x+2 x−2 ∣x−6∣ −x+6 x−6 x−6 x−6 f(x) x−13 −x−1 x+9 −x+13 so x<−6 ⇒f(x)=x−13 ⇒f^′ (x)=1 −6<x<2 ⇒f(x)=−x−1 ⇒f^′ (x)=−1 −5<x<2⇒f(x)=x+9 ⇒f^′ (x)=1 x>2 ⇒f(x)=−x+13 ⇒f^′ (x)=−1
$${x}\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\infty\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{6}\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{5}\:\:\:\:\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:+\infty \\ $$$$\mid{x}+\mathrm{5}\mid\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−{x}−\mathrm{5}\:\:\:\:\:\:\:−{x}−\mathrm{5}\:\:\:{x}+\mathrm{5}\:\:\:\:\:\:{x}+\mathrm{5} \\ $$$$\mid{x}−\mathrm{2}\mid\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−{x}+\mathrm{2}\:\:\:\:\:\:\:\:\:\:−{x}+\mathrm{2}\:\:\:\:−{x}+\mathrm{2}\:\:\:\:\:{x}−\mathrm{2} \\ $$$$\mid{x}−\mathrm{6}\mid\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−{x}+\mathrm{6}\:\:\:\:\:\:\:{x}−\mathrm{6}\:\:\:\:\:\:\:\:\:\:{x}−\mathrm{6}\:\:\:\:\:\:\:\:\:{x}−\mathrm{6} \\ $$$${f}\left({x}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}−\mathrm{13}\:\:\:\:\:\:\:\:−{x}−\mathrm{1}\:\:\:\:\:{x}+\mathrm{9}\:\:\:\:\:\:\:−{x}+\mathrm{13} \\ $$$${so}\:\:{x}<−\mathrm{6}\:\Rightarrow{f}\left({x}\right)={x}−\mathrm{13}\:\Rightarrow{f}^{'} \left({x}\right)=\mathrm{1} \\ $$$$−\mathrm{6}<{x}<\mathrm{2}\:\Rightarrow{f}\left({x}\right)=−{x}−\mathrm{1}\:\Rightarrow{f}^{'} \left({x}\right)=−\mathrm{1} \\ $$$$−\mathrm{5}<{x}<\mathrm{2}\Rightarrow{f}\left({x}\right)={x}+\mathrm{9}\:\Rightarrow{f}^{'} \left({x}\right)=\mathrm{1} \\ $$$${x}>\mathrm{2}\:\Rightarrow{f}\left({x}\right)=−{x}+\mathrm{13}\:\Rightarrow{f}^{'} \left({x}\right)=−\mathrm{1} \\ $$
Answered by mind is power last updated on 04/Dec/19
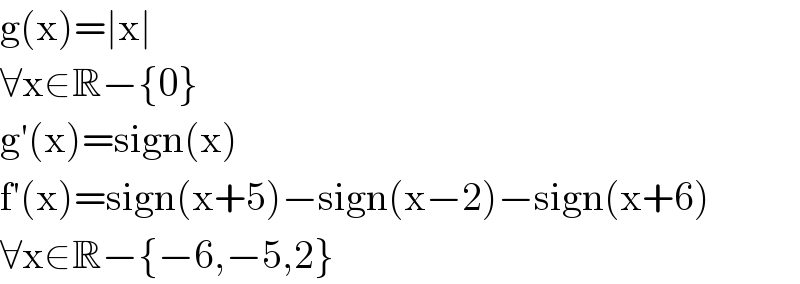
g(x)=∣x∣ ∀x∈R−{0} g′(x)=sign(x) f′(x)=sign(x+5)−sign(x−2)−sign(x+6) ∀x∈R−{−6,−5,2}
$$\mathrm{g}\left(\mathrm{x}\right)=\mid\mathrm{x}\mid \\ $$$$\forall\mathrm{x}\in\mathbb{R}−\left\{\mathrm{0}\right\} \\ $$$$\mathrm{g}'\left(\mathrm{x}\right)=\mathrm{sign}\left(\mathrm{x}\right) \\ $$$$\mathrm{f}'\left(\mathrm{x}\right)=\mathrm{sign}\left(\mathrm{x}+\mathrm{5}\right)−\mathrm{sign}\left(\mathrm{x}−\mathrm{2}\right)−\mathrm{sign}\left(\mathrm{x}+\mathrm{6}\right) \\ $$$$\forall\mathrm{x}\in\mathbb{R}−\left\{−\mathrm{6},−\mathrm{5},\mathrm{2}\right\} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *