Menu Close

f-x-x-ln-x-1-e-x-f-x-

Tinku Tara 0 Comments
Pin




Question Number 4993 by love math last updated on 29/Mar/16
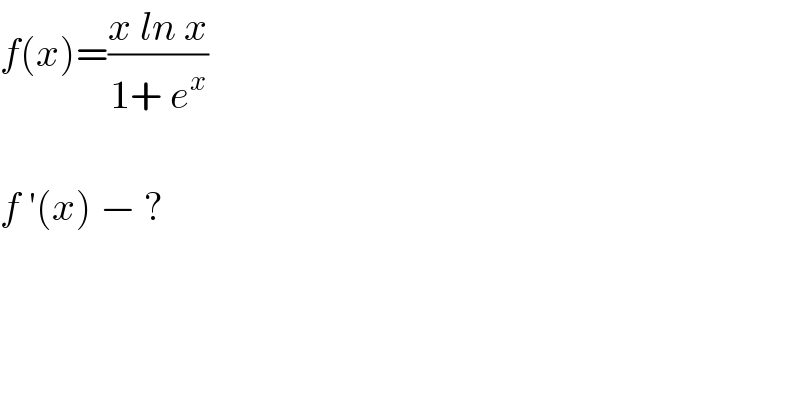
f(x)=((x ln x)/(1+ e^x )) f ′(x) − ?
$${f}\left({x}\right)=\frac{{x}\:{ln}\:{x}}{\mathrm{1}+\:{e}^{{x}} } \\ $$$$ \\ $$$${f}\:'\left({x}\right)\:−\:? \\ $$
Answered by FilupSmith last updated on 30/Mar/16
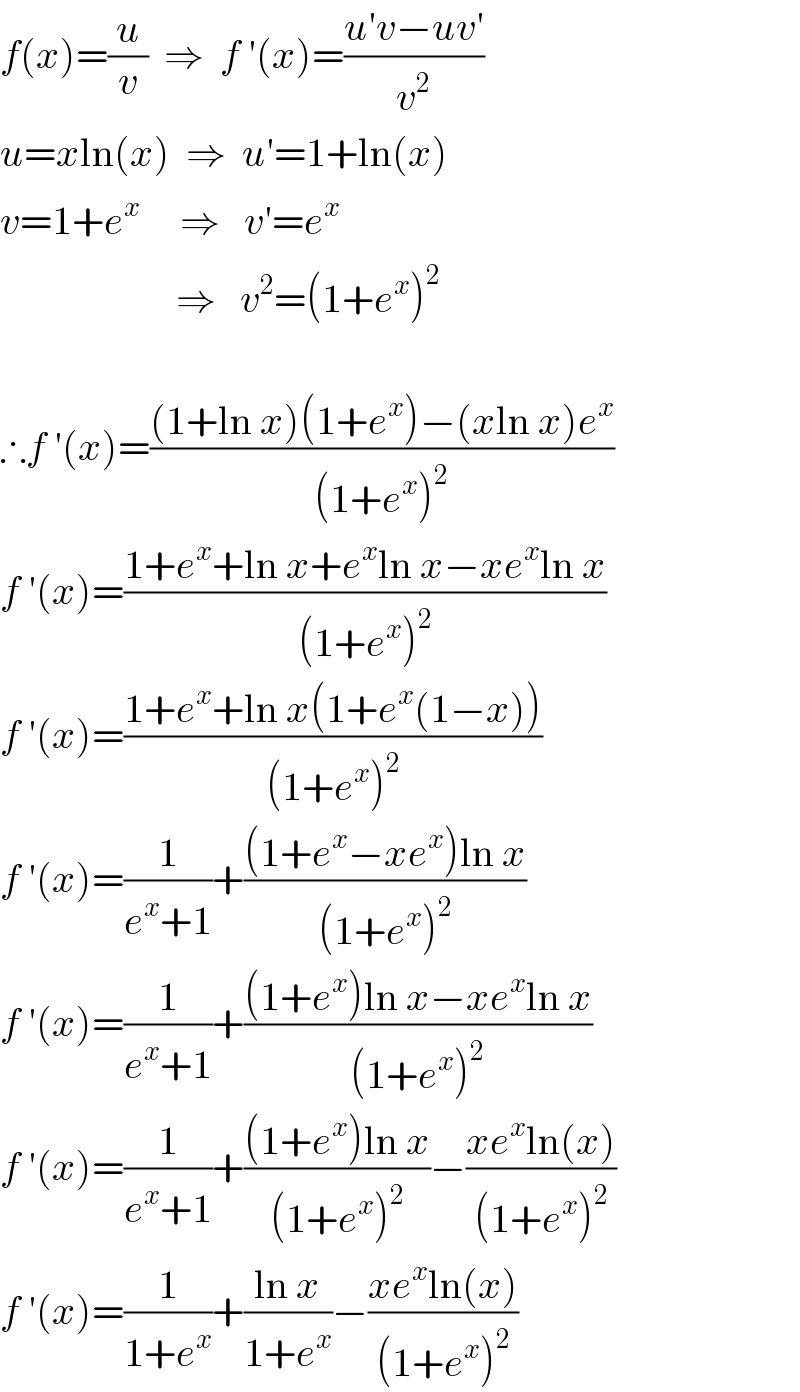
f(x)=(u/v) ⇒ f ′(x)=((u′v−uv′)/v^2 ) u=xln(x) ⇒ u′=1+ln(x) v=1+e^x ⇒ v′=e^x ⇒ v^2 =(1+e^x )^2 ∴f ′(x)=(((1+ln x)(1+e^x )−(xln x)e^x )/((1+e^x )^2 )) f ′(x)=((1+e^x +ln x+e^x ln x−xe^x ln x)/((1+e^x )^2 )) f ′(x)=((1+e^x +ln x(1+e^x (1−x)))/((1+e^x )^2 )) f ′(x)=(1/(e^x +1))+(((1+e^x −xe^x )ln x)/((1+e^x )^2 )) f ′(x)=(1/(e^x +1))+(((1+e^x )ln x−xe^x ln x)/((1+e^x )^2 )) f ′(x)=(1/(e^x +1))+(((1+e^x )ln x)/((1+e^x )^2 ))−((xe^x ln(x))/((1+e^x )^2 )) f ′(x)=(1/(1+e^x ))+((ln x)/(1+e^x ))−((xe^x ln(x))/((1+e^x )^2 ))
$${f}\left({x}\right)=\frac{{u}}{{v}}\:\:\Rightarrow\:\:{f}\:'\left({x}\right)=\frac{{u}'{v}−{uv}'}{{v}^{\mathrm{2}} } \\ $$$${u}={x}\mathrm{ln}\left({x}\right)\:\:\Rightarrow\:\:{u}'=\mathrm{1}+\mathrm{ln}\left({x}\right) \\ $$$${v}=\mathrm{1}+{e}^{{x}} \:\:\:\:\:\Rightarrow\:\:\:{v}'={e}^{{x}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\:\:{v}^{\mathrm{2}} =\left(\mathrm{1}+{e}^{{x}} \right)^{\mathrm{2}} \\ $$$$ \\ $$$$\therefore{f}\:'\left({x}\right)=\frac{\left(\mathrm{1}+\mathrm{ln}\:{x}\right)\left(\mathrm{1}+{e}^{{x}} \right)−\left({x}\mathrm{ln}\:{x}\right){e}^{{x}} }{\left(\mathrm{1}+{e}^{{x}} \right)^{\mathrm{2}} } \\ $$$${f}\:'\left({x}\right)=\frac{\mathrm{1}+{e}^{{x}} +\mathrm{ln}\:{x}+{e}^{{x}} \mathrm{ln}\:{x}−{xe}^{{x}} \mathrm{ln}\:{x}}{\left(\mathrm{1}+{e}^{{x}} \right)^{\mathrm{2}} } \\ $$$${f}\:'\left({x}\right)=\frac{\mathrm{1}+{e}^{{x}} +\mathrm{ln}\:{x}\left(\mathrm{1}+{e}^{{x}} \left(\mathrm{1}−{x}\right)\right)}{\left(\mathrm{1}+{e}^{{x}} \right)^{\mathrm{2}} } \\ $$$${f}\:'\left({x}\right)=\frac{\mathrm{1}}{{e}^{{x}} +\mathrm{1}}+\frac{\left(\mathrm{1}+{e}^{{x}} −{xe}^{{x}} \right)\mathrm{ln}\:{x}}{\left(\mathrm{1}+{e}^{{x}} \right)^{\mathrm{2}} } \\ $$$${f}\:'\left({x}\right)=\frac{\mathrm{1}}{{e}^{{x}} +\mathrm{1}}+\frac{\left(\mathrm{1}+{e}^{{x}} \right)\mathrm{ln}\:{x}−{xe}^{{x}} \mathrm{ln}\:{x}}{\left(\mathrm{1}+{e}^{{x}} \right)^{\mathrm{2}} } \\ $$$${f}\:'\left({x}\right)=\frac{\mathrm{1}}{{e}^{{x}} +\mathrm{1}}+\frac{\left(\mathrm{1}+{e}^{{x}} \right)\mathrm{ln}\:{x}}{\left(\mathrm{1}+{e}^{{x}} \right)^{\mathrm{2}} }−\frac{{xe}^{{x}} \mathrm{ln}\left({x}\right)}{\left(\mathrm{1}+{e}^{{x}} \right)^{\mathrm{2}} } \\ $$$${f}\:'\left({x}\right)=\frac{\mathrm{1}}{\mathrm{1}+{e}^{{x}} }+\frac{\mathrm{ln}\:{x}}{\mathrm{1}+{e}^{{x}} }−\frac{{xe}^{{x}} \mathrm{ln}\left({x}\right)}{\left(\mathrm{1}+{e}^{{x}} \right)^{\mathrm{2}} } \\ $$
Commented by FilupSmith last updated on 30/Mar/16
Correct if wrong
$$\mathrm{Correct}\:\mathrm{if}\:\mathrm{wrong} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *