Question Number 70891 by Henri Boucatchou last updated on 09/Oct/19
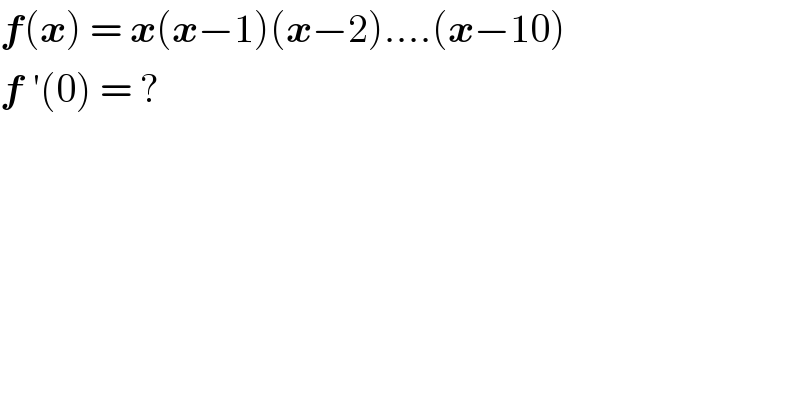
$$\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)\:=\:\boldsymbol{{x}}\left(\boldsymbol{{x}}−\mathrm{1}\right)\left(\boldsymbol{{x}}−\mathrm{2}\right)….\left(\boldsymbol{{x}}−\mathrm{10}\right) \\ $$$$\boldsymbol{{f}}\:'\left(\mathrm{0}\right)\:=\:? \\ $$
Commented by kaivan.ahmadi last updated on 09/Oct/19
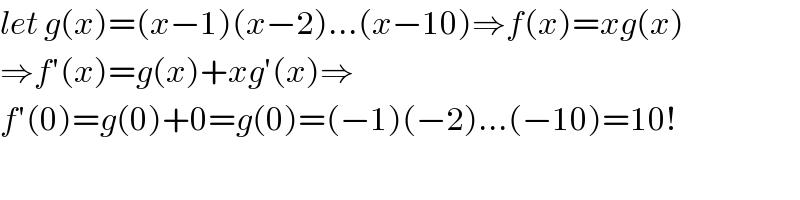
$${let}\:{g}\left({x}\right)=\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)…\left({x}−\mathrm{10}\right)\Rightarrow{f}\left({x}\right)={xg}\left({x}\right) \\ $$$$\Rightarrow{f}'\left({x}\right)={g}\left({x}\right)+{xg}'\left({x}\right)\Rightarrow \\ $$$${f}'\left(\mathrm{0}\right)={g}\left(\mathrm{0}\right)+\mathrm{0}={g}\left(\mathrm{0}\right)=\left(−\mathrm{1}\right)\left(−\mathrm{2}\right)…\left(−\mathrm{10}\right)=\mathrm{10}! \\ $$
Commented by Prithwish sen last updated on 09/Oct/19

$$\mathrm{Excellent}\:\mathrm{Sir}. \\ $$
