Question Number 142443 by Hassen_Timol last updated on 31/May/21
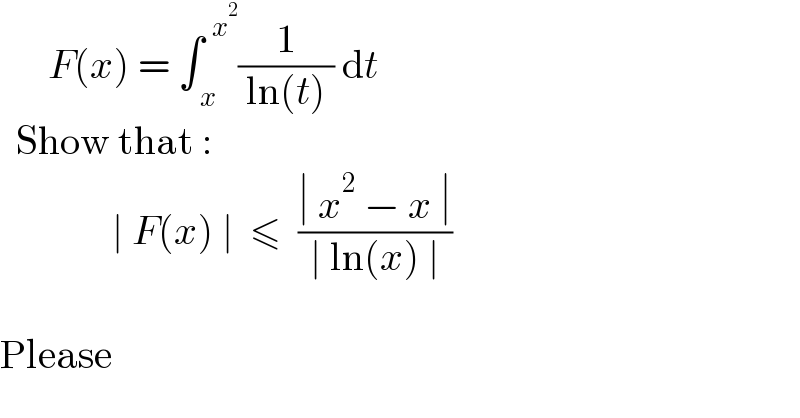
$$\:\:\:\:\:\:{F}\left({x}\right)\:=\:\int_{\:{x}} ^{\:\:{x}^{\mathrm{2}} } \frac{\mathrm{1}}{\:\mathrm{ln}\left({t}\right)\:}\:\mathrm{d}{t} \\ $$$$\:\:\mathrm{Show}\:\mathrm{that}\:: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid\:{F}\left({x}\right)\:\mid\:\:\leqslant\:\:\frac{\mid\:{x}^{\mathrm{2}} \:−\:{x}\:\mid}{\mid\:\mathrm{ln}\left({x}\right)\:\mid} \\ $$$$ \\ $$$$\mathrm{Please} \\ $$
Answered by Boucatchou last updated on 31/May/21
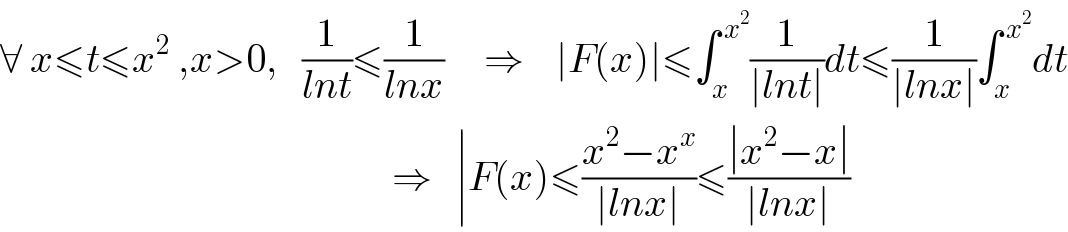
$$\forall\:{x}\leqslant{t}\leqslant{x}^{\mathrm{2}} \:,{x}>\mathrm{0},\:\:\:\frac{\mathrm{1}}{{lnt}}\leqslant\frac{\mathrm{1}}{{lnx}}\:\:\:\:\:\Rightarrow\:\:\:\:\mid{F}\left({x}\right)\mid\leqslant\int_{{x}} ^{\:{x}^{\mathrm{2}} } \frac{\mathrm{1}}{\mid{lnt}\mid}{dt}\leqslant\frac{\mathrm{1}}{\mid{lnx}\mid}\int_{{x}} ^{\:{x}^{\mathrm{2}} } {dt} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\:\:\mid{F}\left({x}\right)\leqslant\frac{{x}^{\mathrm{2}} −{x}^{{x}} }{\mid{lnx}\mid}\leqslant\frac{\mid{x}^{\mathrm{2}} −{x}\mid}{\mid{lnx}\mid} \\ $$
