Question Number 624 by 123456 last updated on 15/Feb/15
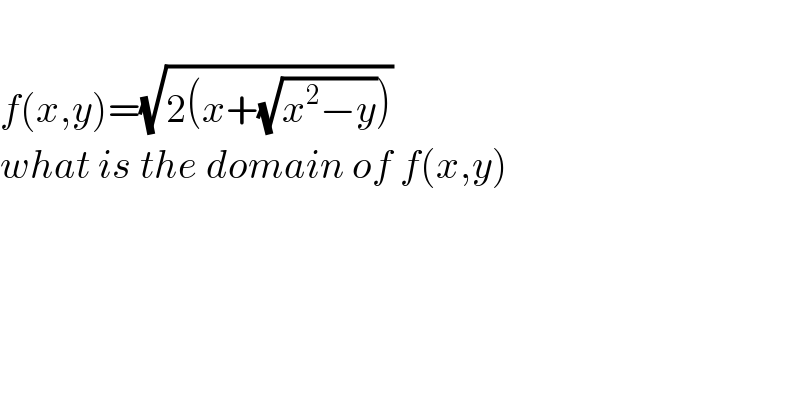
$$ \\ $$$${f}\left({x},{y}\right)=\sqrt{\mathrm{2}\left({x}+\sqrt{{x}^{\mathrm{2}} −{y}}\right)} \\ $$$${what}\:{is}\:{the}\:{domain}\:{of}\:{f}\left({x},{y}\right) \\ $$
Commented by prakash jain last updated on 12/Feb/15
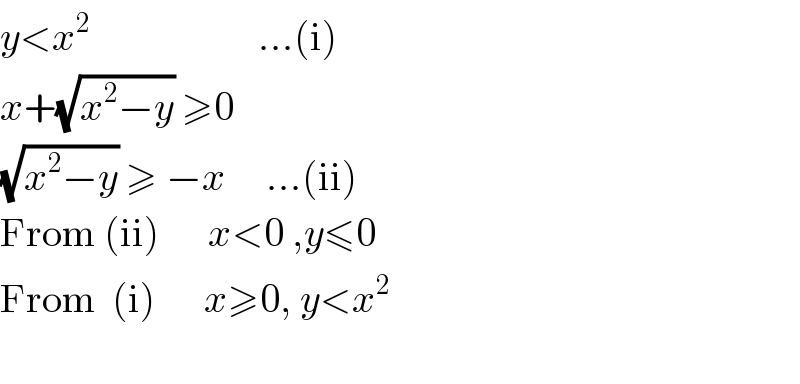
$${y}<{x}^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…\left(\mathrm{i}\right) \\ $$$${x}+\sqrt{{x}^{\mathrm{2}} −{y}}\:\geqslant\mathrm{0}\:\:\: \\ $$$$\sqrt{{x}^{\mathrm{2}} −{y}}\:\geqslant\:−{x}\:\:\:\:\:…\left(\mathrm{ii}\right) \\ $$$$\mathrm{From}\:\left(\mathrm{ii}\right)\:\:\:\:\:\:{x}<\mathrm{0}\:,{y}\leqslant\mathrm{0} \\ $$$$\mathrm{From}\:\:\left(\mathrm{i}\right)\:\:\:\:\:\:{x}\geqslant\mathrm{0},\:{y}<{x}^{\mathrm{2}} \\ $$$$ \\ $$
Answered by prakash jain last updated on 15/Feb/15

$$\left\{\left({x},{y}\right)\in\mathbb{R}^{\mathrm{2}} :{x}^{\mathrm{2}} \geqslant{y}\:\mathrm{and}\:{x}+\sqrt{{x}^{\mathrm{2}} −{y}\:}\:\geqslant\mathrm{0}\right\} \\ $$
