Menu Close

f-x-y-f-x-1-y-x-1-f-x-y-ye-x-x-0-f-5-6-

Tinku Tara 0 Comments
Pin




Question Number 2604 by 123456 last updated on 23/Nov/15
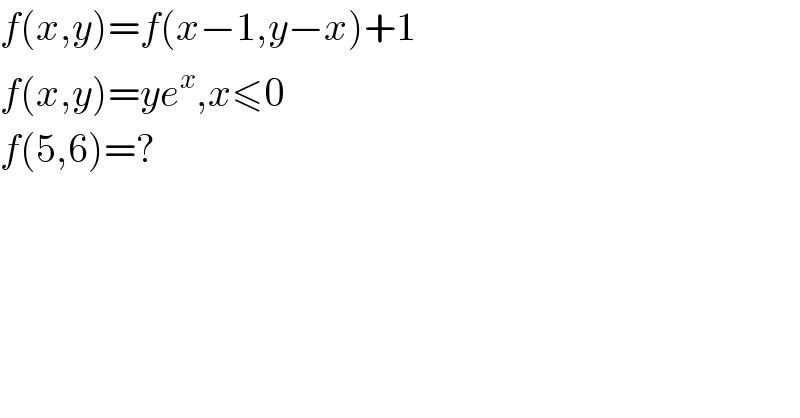
f(x,y)=f(x−1,y−x)+1 f(x,y)=ye^x ,x≤0 f(5,6)=?
$${f}\left({x},{y}\right)={f}\left({x}−\mathrm{1},{y}−{x}\right)+\mathrm{1} \\ $$$${f}\left({x},{y}\right)={ye}^{{x}} ,{x}\leqslant\mathrm{0} \\ $$$${f}\left(\mathrm{5},\mathrm{6}\right)=? \\ $$
Answered by Yozzis last updated on 23/Nov/15
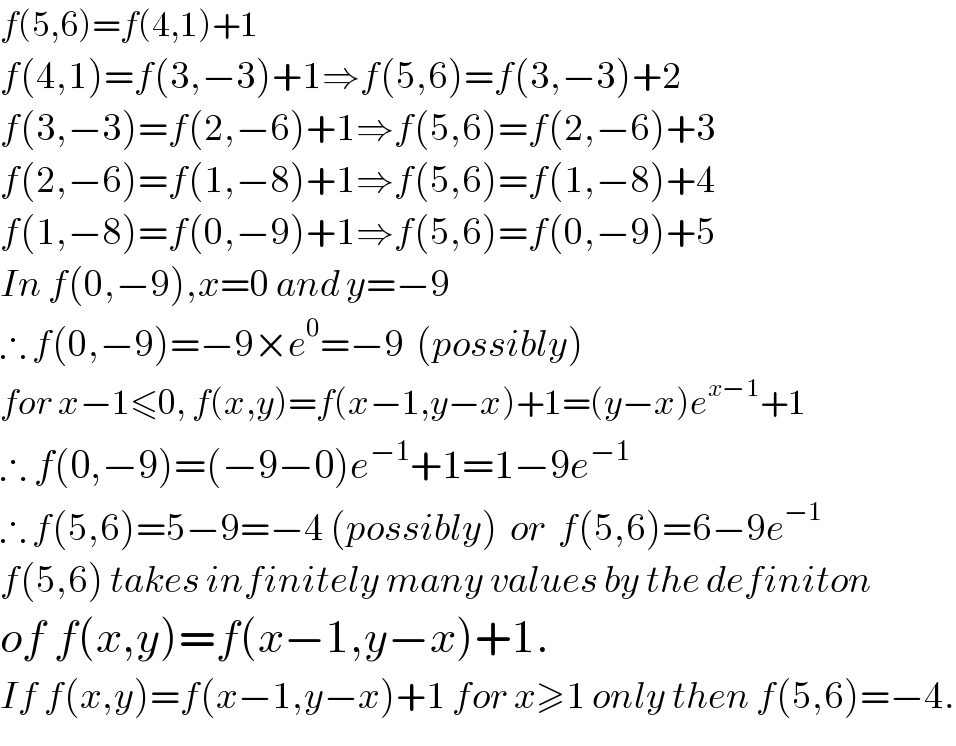
f(5,6)=f(4,1)+1 f(4,1)=f(3,−3)+1⇒f(5,6)=f(3,−3)+2 f(3,−3)=f(2,−6)+1⇒f(5,6)=f(2,−6)+3 f(2,−6)=f(1,−8)+1⇒f(5,6)=f(1,−8)+4 f(1,−8)=f(0,−9)+1⇒f(5,6)=f(0,−9)+5 In f(0,−9),x=0 and y=−9 ∴ f(0,−9)=−9×e^0 =−9 (possibly) for x−1≤0, f(x,y)=f(x−1,y−x)+1=(y−x)e^(x−1) +1 ∴ f(0,−9)=(−9−0)e^(−1) +1=1−9e^(−1) ∴ f(5,6)=5−9=−4 (possibly) or f(5,6)=6−9e^(−1) f(5,6) takes infinitely many values by the definiton of f(x,y)=f(x−1,y−x)+1. If f(x,y)=f(x−1,y−x)+1 for x≥1 only then f(5,6)=−4.
$${f}\left(\mathrm{5},\mathrm{6}\right)={f}\left(\mathrm{4},\mathrm{1}\right)+\mathrm{1} \\ $$$${f}\left(\mathrm{4},\mathrm{1}\right)={f}\left(\mathrm{3},−\mathrm{3}\right)+\mathrm{1}\Rightarrow{f}\left(\mathrm{5},\mathrm{6}\right)={f}\left(\mathrm{3},−\mathrm{3}\right)+\mathrm{2} \\ $$$${f}\left(\mathrm{3},−\mathrm{3}\right)={f}\left(\mathrm{2},−\mathrm{6}\right)+\mathrm{1}\Rightarrow{f}\left(\mathrm{5},\mathrm{6}\right)={f}\left(\mathrm{2},−\mathrm{6}\right)+\mathrm{3} \\ $$$${f}\left(\mathrm{2},−\mathrm{6}\right)={f}\left(\mathrm{1},−\mathrm{8}\right)+\mathrm{1}\Rightarrow{f}\left(\mathrm{5},\mathrm{6}\right)={f}\left(\mathrm{1},−\mathrm{8}\right)+\mathrm{4} \\ $$$${f}\left(\mathrm{1},−\mathrm{8}\right)={f}\left(\mathrm{0},−\mathrm{9}\right)+\mathrm{1}\Rightarrow{f}\left(\mathrm{5},\mathrm{6}\right)={f}\left(\mathrm{0},−\mathrm{9}\right)+\mathrm{5} \\ $$$${In}\:{f}\left(\mathrm{0},−\mathrm{9}\right),{x}=\mathrm{0}\:{and}\:{y}=−\mathrm{9} \\ $$$$\therefore\:{f}\left(\mathrm{0},−\mathrm{9}\right)=−\mathrm{9}×{e}^{\mathrm{0}} =−\mathrm{9}\:\:\left({possibly}\right) \\ $$$${for}\:{x}−\mathrm{1}\leqslant\mathrm{0},\:{f}\left({x},{y}\right)={f}\left({x}−\mathrm{1},{y}−{x}\right)+\mathrm{1}=\left({y}−{x}\right){e}^{{x}−\mathrm{1}} +\mathrm{1} \\ $$$$\therefore\:{f}\left(\mathrm{0},−\mathrm{9}\right)=\left(−\mathrm{9}−\mathrm{0}\right){e}^{−\mathrm{1}} +\mathrm{1}=\mathrm{1}−\mathrm{9}{e}^{−\mathrm{1}} \\ $$$$\therefore\:{f}\left(\mathrm{5},\mathrm{6}\right)=\mathrm{5}−\mathrm{9}=−\mathrm{4}\:\left({possibly}\right)\:\:{or}\:\:{f}\left(\mathrm{5},\mathrm{6}\right)=\mathrm{6}−\mathrm{9}{e}^{−\mathrm{1}} \\ $$$${f}\left(\mathrm{5},\mathrm{6}\right)\:{takes}\:{infinitely}\:{many}\:{values}\:{by}\:{the}\:{definiton} \\ $$$${of}\:{f}\left({x},{y}\right)={f}\left({x}−\mathrm{1},{y}−{x}\right)+\mathrm{1}. \\ $$$${If}\:{f}\left({x},{y}\right)={f}\left({x}−\mathrm{1},{y}−{x}\right)+\mathrm{1}\:{for}\:{x}\geqslant\mathrm{1}\:{only}\:{then}\:{f}\left(\mathrm{5},\mathrm{6}\right)=−\mathrm{4}. \\ $$
Commented by prakash jain last updated on 23/Nov/15
The font looks really small.
$$\mathrm{The}\:\mathrm{font}\:\mathrm{looks}\:\mathrm{really}\:\mathrm{small}.\: \\ $$
Commented by Yozzis last updated on 23/Nov/15
I don′t know why this has happened...
$${I}\:{don}'{t}\:{know}\:{why}\:{this}\:{has}\:{happened}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *