Question Number 419 by 123456 last updated on 25/Jan/15
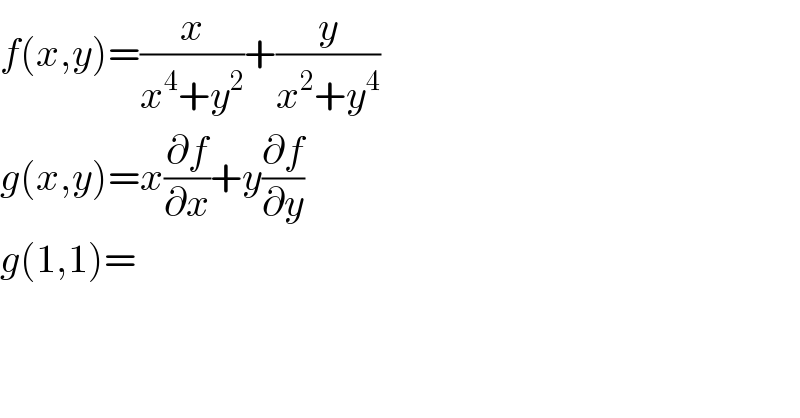
$${f}\left({x},{y}\right)=\frac{{x}}{{x}^{\mathrm{4}} +{y}^{\mathrm{2}} }+\frac{{y}}{{x}^{\mathrm{2}} +{y}^{\mathrm{4}} } \\ $$$${g}\left({x},{y}\right)={x}\frac{\partial{f}}{\partial{x}}+{y}\frac{\partial{f}}{\partial{y}} \\ $$$${g}\left(\mathrm{1},\mathrm{1}\right)= \\ $$
Answered by 9999 last updated on 01/Jan/15
![(∂f/∂x)=(((x^4 +y^2 )−x(4x^3 ))/((x^4 +y^2 )^2 )) − ((2xy)/((x^2 +y^4 )^2 )) x(∂f/∂x)=1.[((2−4)/4) − (2/4)]= −(1/2)−(1/2)= −1 y (∂f/∂x)=−1 x(∂f/∂x)+y(∂f/∂y)=−2](https://www.tinkutara.com/question/Q423.png)
$$\frac{\partial{f}}{\partial{x}}=\frac{\left({x}^{\mathrm{4}} +{y}^{\mathrm{2}} \right)−{x}\left(\mathrm{4}{x}^{\mathrm{3}} \right)}{\left({x}^{\mathrm{4}} +{y}^{\mathrm{2}} \right)^{\mathrm{2}} }\:−\:\frac{\mathrm{2}{xy}}{\left({x}^{\mathrm{2}} +{y}^{\mathrm{4}} \right)^{\mathrm{2}} } \\ $$$${x}\frac{\partial{f}}{\partial{x}}=\mathrm{1}.\left[\frac{\mathrm{2}−\mathrm{4}}{\mathrm{4}}\:−\:\frac{\mathrm{2}}{\mathrm{4}}\right]=\:−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}=\:−\mathrm{1} \\ $$$${y}\:\frac{\partial{f}}{\partial{x}}=−\mathrm{1} \\ $$$${x}\frac{\partial{f}}{\partial{x}}+{y}\frac{\partial{f}}{\partial{y}}=−\mathrm{2} \\ $$
