Menu Close

f-x-y-x-y-2-x-2-y-2-f-u-f-v-x-uv-y-u-v-

Tinku Tara
Pin




Question Number 424 by 123456 last updated on 25/Jan/15
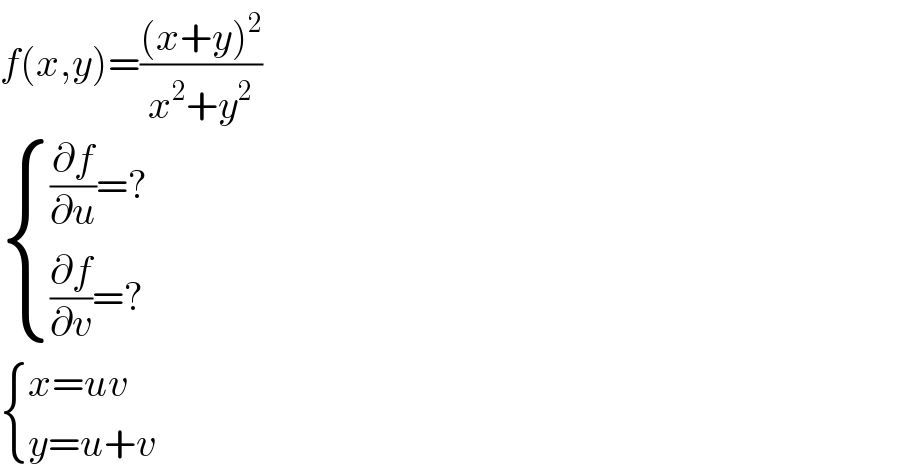
f(x,y)=(((x+y)^2 )/(x^2 +y^2 )) { (((∂f/∂u)=?)),(((∂f/∂v)=?)) :} { ((x=uv)),((y=u+v)) :}
$${f}\left({x},{y}\right)=\frac{\left({x}+{y}\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$$\begin{cases}{\frac{\partial{f}}{\partial{u}}=?}\\{\frac{\partial{f}}{\partial{v}}=?}\end{cases} \\ $$$$\begin{cases}{{x}={uv}}\\{{y}={u}+{v}}\end{cases} \\ $$
Answered by prakash jain last updated on 02/Jan/15
f(u,v)=1+((2xy)/(x^2 +y^2 )) = 1+((2u^2 v+2uv^2 )/((uv)^2 +(u+v)^2 )) (∂f/∂u)=(([(uv)^2 +(u+v)^2 ][4uv+2v^2 ]−(2u^2 v+2uv^2 )(2uv+2u+2v))/([(uv)^2 +(u+v)^2 ]^2 )) Simplification 4u^3 v^3 +4u^3 v+8u^2 v^2 +4uv^3 +2u^2 v^4 +2u^2 v^2 +4uv^3 +2v^4 −4u^3 v^2 −4u^2 v^3 −4u^3 v−4u^2 v^2 −4u^2 v^2 −4uv^3 =4u^3 v^3 +2u^2 v^4 +2u^2 v^2 +4uv^3 +2v^4 −4u^3 v^2 −4u^2 v^3 (∂f/∂u)=((4u^3 v^3 +2u^2 v^4 +2u^2 v^2 +4uv^3 +2v^4 −4u^3 v^2 −4u^2 v^3 )/([(uv)^2 +(u+v)^2 ]^2 )) (∂f/∂v)=((4u^3 v^3 +2v^2 u^4 +2u^2 v^2 +4vu^3 +2u^4 −4v^3 u^2 −4v^2 u^3 )/([(uv)^2 +(u+v)^2 ]^2 ))
$${f}\left({u},{v}\right)=\mathrm{1}+\frac{\mathrm{2}{xy}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \:}\:=\:\mathrm{1}+\frac{\mathrm{2}{u}^{\mathrm{2}} {v}+\mathrm{2}{uv}^{\mathrm{2}} }{\left({uv}\right)^{\mathrm{2}} +\left({u}+{v}\right)^{\mathrm{2}} } \\ $$$$\frac{\partial{f}}{\partial{u}}=\frac{\left[\left({uv}\right)^{\mathrm{2}} +\left({u}+{v}\right)^{\mathrm{2}} \right]\left[\mathrm{4}{uv}+\mathrm{2}{v}^{\mathrm{2}} \right]−\left(\mathrm{2}{u}^{\mathrm{2}} {v}+\mathrm{2}{uv}^{\mathrm{2}} \right)\left(\mathrm{2}{uv}+\mathrm{2}{u}+\mathrm{2}{v}\right)}{\left[\left({uv}\right)^{\mathrm{2}} +\left({u}+{v}\right)^{\mathrm{2}} \right]^{\mathrm{2}} } \\ $$$${Simplification} \\ $$$$\mathrm{4}{u}^{\mathrm{3}} {v}^{\mathrm{3}} +\mathrm{4}{u}^{\mathrm{3}} {v}+\mathrm{8}{u}^{\mathrm{2}} {v}^{\mathrm{2}} +\mathrm{4}{uv}^{\mathrm{3}} +\mathrm{2}{u}^{\mathrm{2}} {v}^{\mathrm{4}} +\mathrm{2}{u}^{\mathrm{2}} {v}^{\mathrm{2}} +\mathrm{4}{uv}^{\mathrm{3}} +\mathrm{2}{v}^{\mathrm{4}} \\ $$$$−\mathrm{4}{u}^{\mathrm{3}} {v}^{\mathrm{2}} −\mathrm{4}{u}^{\mathrm{2}} {v}^{\mathrm{3}} −\mathrm{4}{u}^{\mathrm{3}} {v}−\mathrm{4}{u}^{\mathrm{2}} {v}^{\mathrm{2}} −\mathrm{4}{u}^{\mathrm{2}} {v}^{\mathrm{2}} −\mathrm{4}{uv}^{\mathrm{3}} \\ $$$$=\mathrm{4}{u}^{\mathrm{3}} {v}^{\mathrm{3}} +\mathrm{2}{u}^{\mathrm{2}} {v}^{\mathrm{4}} +\mathrm{2}{u}^{\mathrm{2}} {v}^{\mathrm{2}} +\mathrm{4}{uv}^{\mathrm{3}} +\mathrm{2}{v}^{\mathrm{4}} −\mathrm{4}{u}^{\mathrm{3}} {v}^{\mathrm{2}} −\mathrm{4}{u}^{\mathrm{2}} {v}^{\mathrm{3}} \\ $$$$\frac{\partial{f}}{\partial{u}}=\frac{\mathrm{4}{u}^{\mathrm{3}} {v}^{\mathrm{3}} +\mathrm{2}{u}^{\mathrm{2}} {v}^{\mathrm{4}} +\mathrm{2}{u}^{\mathrm{2}} {v}^{\mathrm{2}} +\mathrm{4}{uv}^{\mathrm{3}} +\mathrm{2}{v}^{\mathrm{4}} −\mathrm{4}{u}^{\mathrm{3}} {v}^{\mathrm{2}} −\mathrm{4}{u}^{\mathrm{2}} {v}^{\mathrm{3}} }{\left[\left({uv}\right)^{\mathrm{2}} +\left({u}+{v}\right)^{\mathrm{2}} \right]^{\mathrm{2}} } \\ $$$$\frac{\partial{f}}{\partial{v}}=\frac{\mathrm{4}{u}^{\mathrm{3}} {v}^{\mathrm{3}} +\mathrm{2}{v}^{\mathrm{2}} {u}^{\mathrm{4}} +\mathrm{2}{u}^{\mathrm{2}} {v}^{\mathrm{2}} +\mathrm{4}{vu}^{\mathrm{3}} +\mathrm{2}{u}^{\mathrm{4}} −\mathrm{4}{v}^{\mathrm{3}} {u}^{\mathrm{2}} −\mathrm{4}{v}^{\mathrm{2}} {u}^{\mathrm{3}} }{\left[\left({uv}\right)^{\mathrm{2}} +\left({u}+{v}\right)^{\mathrm{2}} \right]^{\mathrm{2}} } \\ $$

Pin