Menu Close

f-x-y-z-y-2-z-3-1-x-xz-3-1-y-2-xy-2-1-z-3-find-f-x-f-y-f-z-

Tinku Tara
Pin




Question Number 303 by 123456 last updated on 25/Jan/15
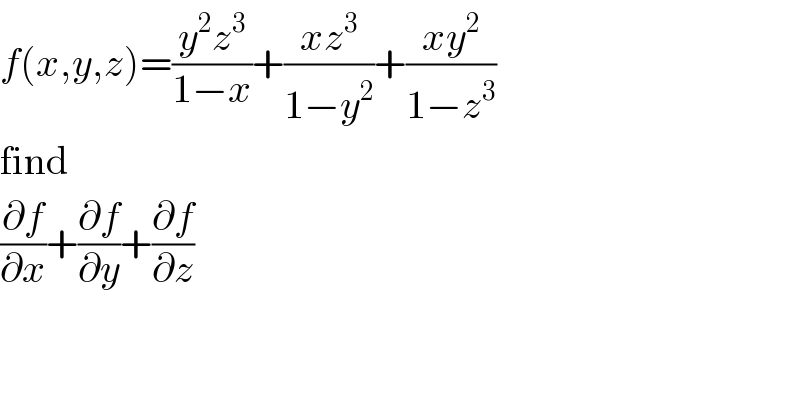
f(x,y,z)=((y^2 z^3 )/(1−x))+((xz^3 )/(1−y^2 ))+((xy^2 )/(1−z^3 )) find (∂f/∂x)+(∂f/∂y)+(∂f/∂z)
$${f}\left({x},{y},{z}\right)=\frac{{y}^{\mathrm{2}} {z}^{\mathrm{3}} }{\mathrm{1}−{x}}+\frac{{xz}^{\mathrm{3}} }{\mathrm{1}−{y}^{\mathrm{2}} }+\frac{{xy}^{\mathrm{2}} }{\mathrm{1}−{z}^{\mathrm{3}} } \\ $$$$\mathrm{find} \\ $$$$\frac{\partial{f}}{\partial{x}}+\frac{\partial{f}}{\partial{y}}+\frac{\partial{f}}{\partial{z}} \\ $$
Answered by prakash jain last updated on 20/Dec/14
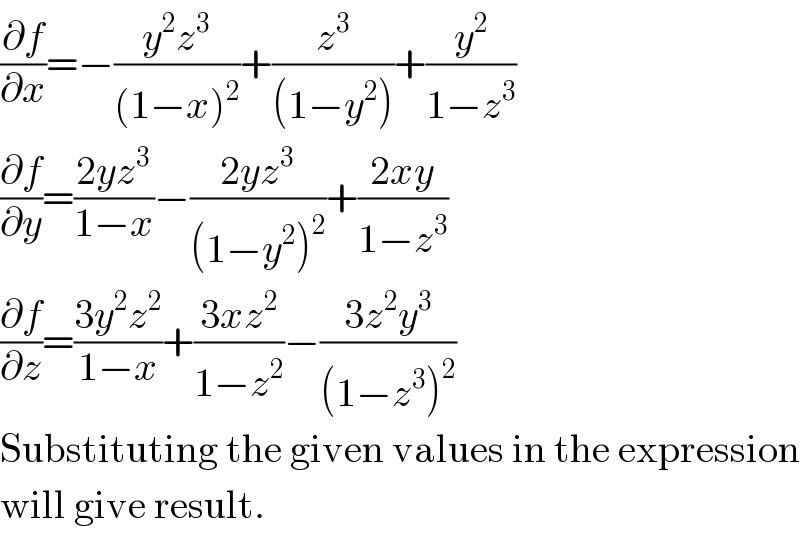
(∂f/∂x)=−((y^2 z^3 )/((1−x)^2 ))+(z^3 /((1−y^2 )))+(y^2 /(1−z^3 )) (∂f/∂y)=((2yz^3 )/(1−x))−((2yz^3 )/((1−y^2 )^2 ))+((2xy)/(1−z^3 )) (∂f/∂z)=((3y^2 z^2 )/(1−x))+((3xz^2 )/(1−z^2 ))−((3z^2 y^3 )/((1−z^3 )^2 )) Substituting the given values in the expression will give result.
$$\frac{\partial{f}}{\partial{x}}=−\frac{{y}^{\mathrm{2}} {z}^{\mathrm{3}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }+\frac{{z}^{\mathrm{3}} }{\left(\mathrm{1}−{y}^{\mathrm{2}} \right)}+\frac{{y}^{\mathrm{2}} }{\mathrm{1}−{z}^{\mathrm{3}} } \\ $$$$\frac{\partial{f}}{\partial{y}}=\frac{\mathrm{2}{yz}^{\mathrm{3}} }{\mathrm{1}−{x}}−\frac{\mathrm{2}{yz}^{\mathrm{3}} }{\left(\mathrm{1}−{y}^{\mathrm{2}} \right)^{\mathrm{2}} }+\frac{\mathrm{2}{xy}}{\mathrm{1}−{z}^{\mathrm{3}} } \\ $$$$\frac{\partial{f}}{\partial{z}}=\frac{\mathrm{3}{y}^{\mathrm{2}} {z}^{\mathrm{2}} }{\mathrm{1}−{x}}+\frac{\mathrm{3}{xz}^{\mathrm{2}} }{\mathrm{1}−{z}^{\mathrm{2}} }−\frac{\mathrm{3}{z}^{\mathrm{2}} {y}^{\mathrm{3}} }{\left(\mathrm{1}−{z}^{\mathrm{3}} \right)^{\mathrm{2}} } \\ $$$$\mathrm{Substituting}\:\mathrm{the}\:\mathrm{given}\:\mathrm{values}\:\mathrm{in}\:\mathrm{the}\:\mathrm{expression} \\ $$$$\mathrm{will}\:\mathrm{give}\:\mathrm{result}. \\ $$

Pin