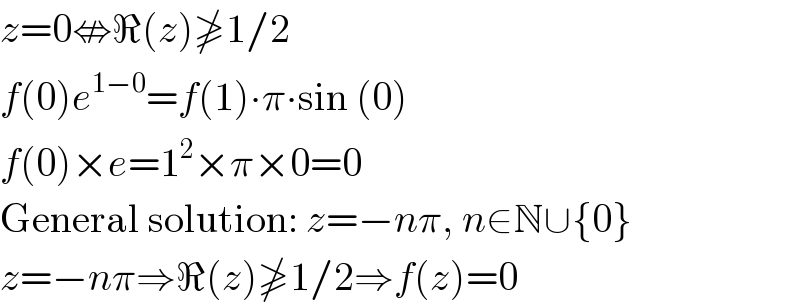Question Number 2344 by 123456 last updated on 17/Nov/15
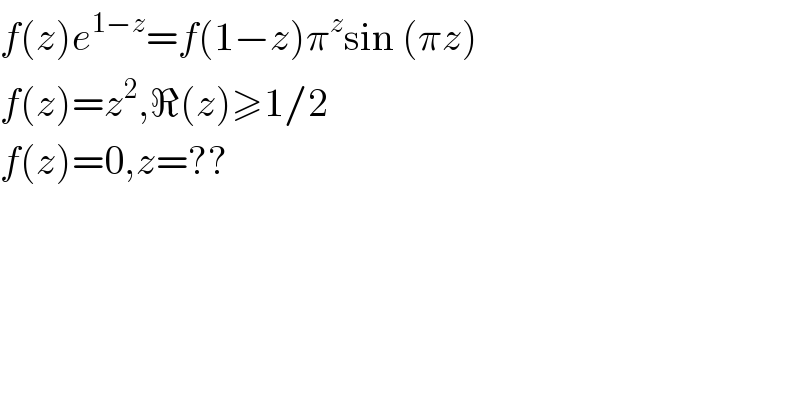
Commented by Yozzi last updated on 17/Nov/15
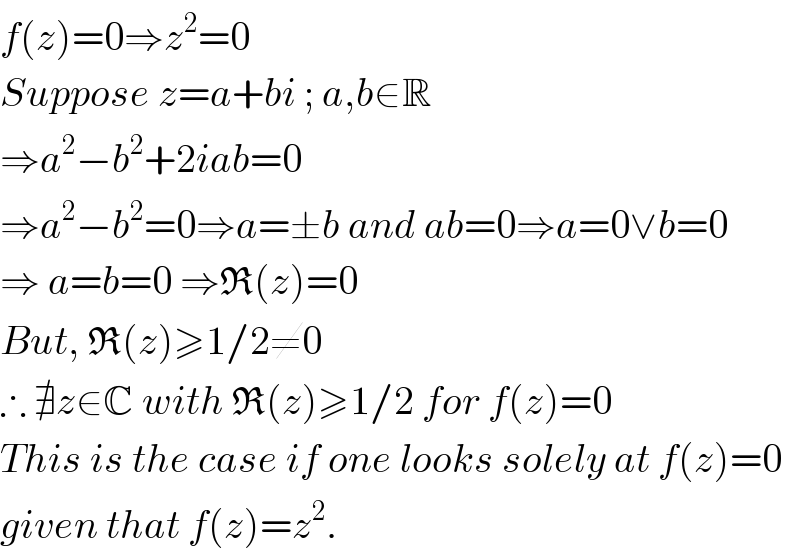
Commented by Yozzi last updated on 17/Nov/15
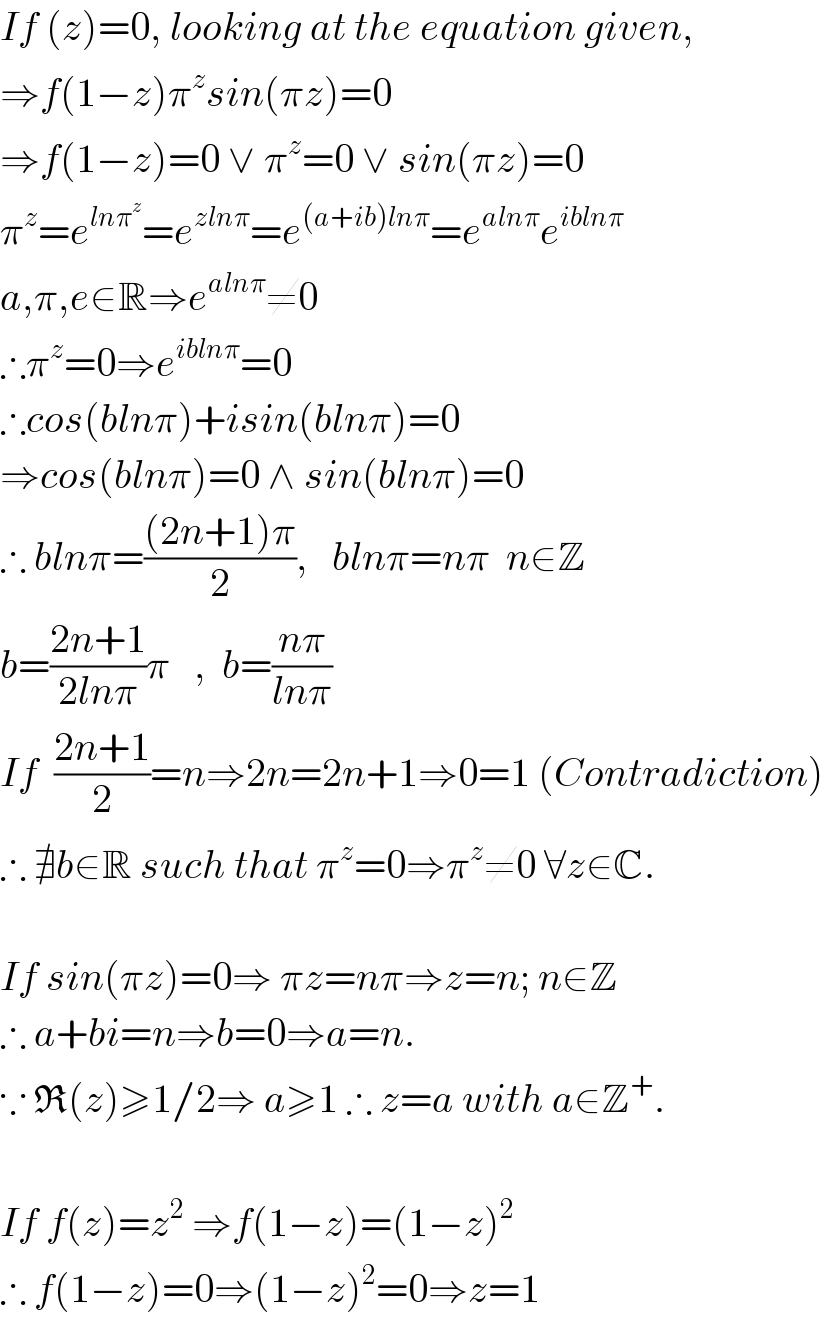
Commented by RasheedAhmad last updated on 17/Nov/15

Commented by RasheedAhmad last updated on 17/Nov/15
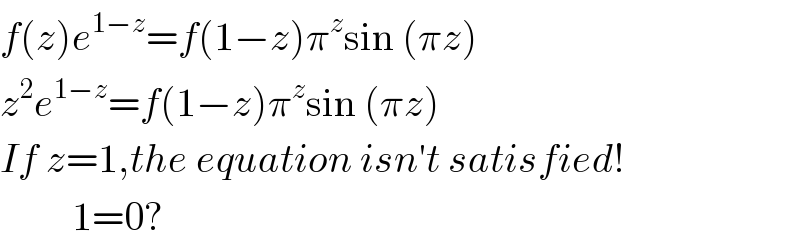
Commented by Yozzi last updated on 17/Nov/15

Commented by Yozzi last updated on 17/Nov/15
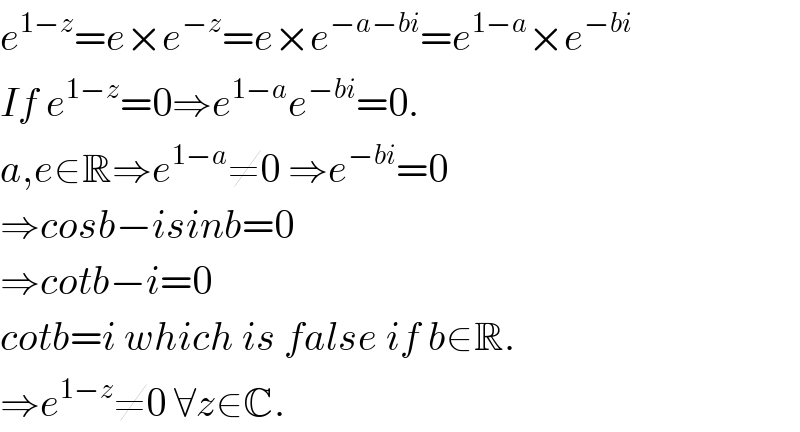
Commented by prakash jain last updated on 17/Nov/15
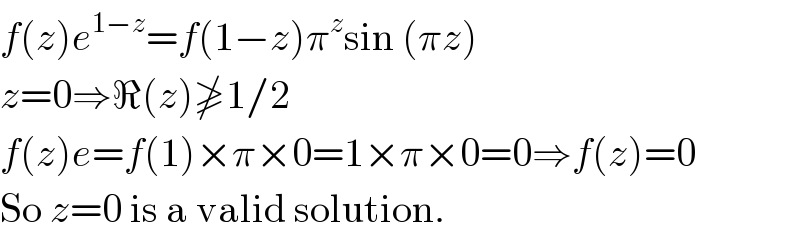
Commented by Yozzi last updated on 17/Nov/15

Answered by prakash jain last updated on 17/Nov/15