Question Number 71666 by aliesam last updated on 18/Oct/19

$${f}:{z}\rightarrow{z} \\ $$$$ \\ $$$${f}\left({x}+{y}\right)={f}\left({x}\right)+{f}\left({y}\right)+\mathrm{3}\left(\mathrm{4}{xy}−\mathrm{1}\right) \\ $$$$ \\ $$$$,{f}\left(\mathrm{1}\right)=\mathrm{0} \\ $$$$ \\ $$$$\forall{x},{y}\:\in{z} \\ $$$${evaluate}\:{f}\left(\mathrm{19}\right) \\ $$
Commented by kaivan.ahmadi last updated on 18/Oct/19
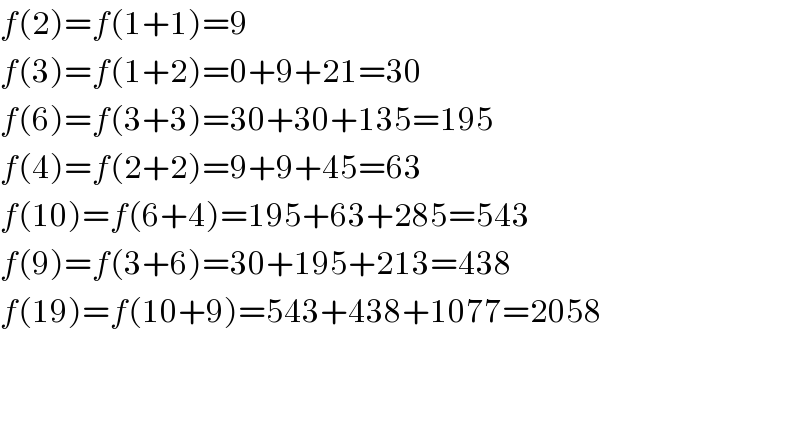
$${f}\left(\mathrm{2}\right)={f}\left(\mathrm{1}+\mathrm{1}\right)=\mathrm{9} \\ $$$${f}\left(\mathrm{3}\right)={f}\left(\mathrm{1}+\mathrm{2}\right)=\mathrm{0}+\mathrm{9}+\mathrm{21}=\mathrm{30} \\ $$$${f}\left(\mathrm{6}\right)={f}\left(\mathrm{3}+\mathrm{3}\right)=\mathrm{30}+\mathrm{30}+\mathrm{135}=\mathrm{195} \\ $$$${f}\left(\mathrm{4}\right)={f}\left(\mathrm{2}+\mathrm{2}\right)=\mathrm{9}+\mathrm{9}+\mathrm{45}=\mathrm{63} \\ $$$${f}\left(\mathrm{10}\right)={f}\left(\mathrm{6}+\mathrm{4}\right)=\mathrm{195}+\mathrm{63}+\mathrm{285}=\mathrm{543} \\ $$$${f}\left(\mathrm{9}\right)={f}\left(\mathrm{3}+\mathrm{6}\right)=\mathrm{30}+\mathrm{195}+\mathrm{213}=\mathrm{438} \\ $$$${f}\left(\mathrm{19}\right)={f}\left(\mathrm{10}+\mathrm{9}\right)=\mathrm{543}+\mathrm{438}+\mathrm{1077}=\mathrm{2058} \\ $$$$ \\ $$$$ \\ $$
Answered by mind is power last updated on 18/Oct/19
![f(x+1)=f(x)+3(4x−3)=f(x)+12x−3 ⇒f(x+1)−f(x)=12x−3 ∀x∈Z ⇒Σ_(x=1) ^(18) [f(x+1)−f(x)]=Σ_(x=1) ^(18) (12x−9) ⇒f(19)−f(1)=((12+12.18)/2).18−3.18 ⇒f(19)=9(12+216)−54=1998](https://www.tinkutara.com/question/Q71668.png)
$$\mathrm{f}\left(\mathrm{x}+\mathrm{1}\right)=\mathrm{f}\left(\mathrm{x}\right)+\mathrm{3}\left(\mathrm{4x}−\mathrm{3}\right)=\mathrm{f}\left(\mathrm{x}\right)+\mathrm{12x}−\mathrm{3} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}+\mathrm{1}\right)−\mathrm{f}\left(\mathrm{x}\right)=\mathrm{12x}−\mathrm{3}\:\:\forall\mathrm{x}\in\mathbb{Z} \\ $$$$\Rightarrow\underset{\mathrm{x}=\mathrm{1}} {\overset{\mathrm{18}} {\sum}}\left[\mathrm{f}\left(\mathrm{x}+\mathrm{1}\right)−\mathrm{f}\left(\mathrm{x}\right)\right]=\underset{\mathrm{x}=\mathrm{1}} {\overset{\mathrm{18}} {\sum}}\left(\mathrm{12x}−\mathrm{9}\right) \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{19}\right)−\mathrm{f}\left(\mathrm{1}\right)=\frac{\mathrm{12}+\mathrm{12}.\mathrm{18}}{\mathrm{2}}.\mathrm{18}−\mathrm{3}.\mathrm{18} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{19}\right)=\mathrm{9}\left(\mathrm{12}+\mathrm{216}\right)−\mathrm{54}=\mathrm{1998} \\ $$$$ \\ $$$$ \\ $$
Commented by aliesam last updated on 18/Oct/19

$${thank}\:{you}\:{sir}\:{nice}\:{sol} \\ $$
Commented by mind is power last updated on 18/Oct/19

$$\mathrm{y}'\mathrm{re}\:\mathrm{welcom} \\ $$$$ \\ $$
