Question Number 74164 by MASANJAJ last updated on 19/Nov/19
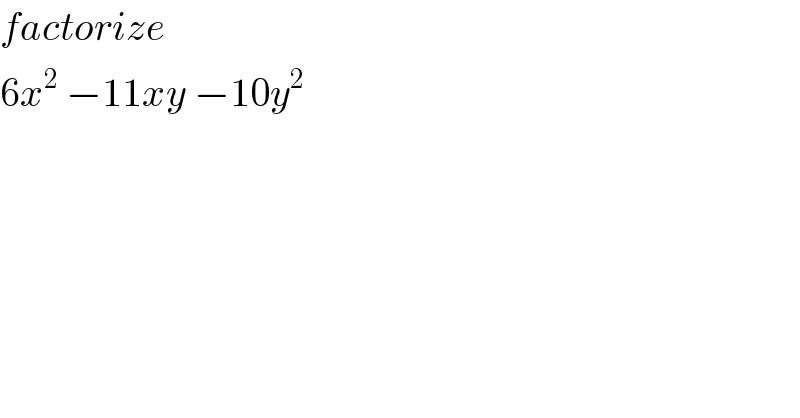
$${factorize} \\ $$$$\mathrm{6}{x}^{\mathrm{2}} \:−\mathrm{11}{xy}\:−\mathrm{10}{y}^{\mathrm{2}} \\ $$
Answered by MJS last updated on 19/Nov/19
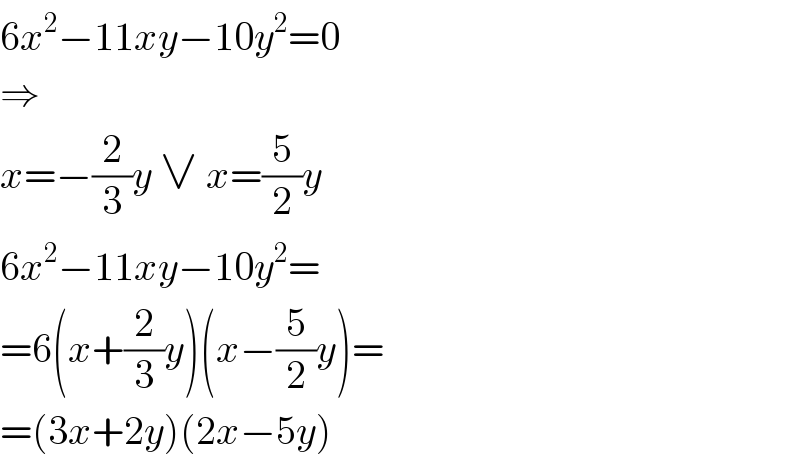
$$\mathrm{6}{x}^{\mathrm{2}} −\mathrm{11}{xy}−\mathrm{10}{y}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow \\ $$$${x}=−\frac{\mathrm{2}}{\mathrm{3}}{y}\:\vee\:{x}=\frac{\mathrm{5}}{\mathrm{2}}{y} \\ $$$$\mathrm{6}{x}^{\mathrm{2}} −\mathrm{11}{xy}−\mathrm{10}{y}^{\mathrm{2}} = \\ $$$$=\mathrm{6}\left({x}+\frac{\mathrm{2}}{\mathrm{3}}{y}\right)\left({x}−\frac{\mathrm{5}}{\mathrm{2}}{y}\right)= \\ $$$$=\left(\mathrm{3}{x}+\mathrm{2}{y}\right)\left(\mathrm{2}{x}−\mathrm{5}{y}\right) \\ $$
Answered by malwaan last updated on 20/Nov/19
![6×(−10)=−60 [⇒4×(−15)] 6x^2 −15xy+4xy−10y^2 =3x(2x−5y)+2y(2x−5y) =(2x−5y)(3x+2y)](https://www.tinkutara.com/question/Q74205.png)
$$\mathrm{6}×\left(−\mathrm{10}\right)=−\mathrm{60}\:\left[\Rightarrow\mathrm{4}×\left(−\mathrm{15}\right)\right] \\ $$$$\mathrm{6}\boldsymbol{{x}}^{\mathrm{2}} \:−\mathrm{15}\boldsymbol{{xy}}+\mathrm{4}\boldsymbol{{xy}}−\mathrm{10}\boldsymbol{{y}}^{\mathrm{2}} \\ $$$$=\mathrm{3}\boldsymbol{{x}}\left(\mathrm{2}\boldsymbol{{x}}−\mathrm{5}\boldsymbol{{y}}\right)+\mathrm{2}\boldsymbol{{y}}\left(\mathrm{2}\boldsymbol{{x}}−\mathrm{5}\boldsymbol{{y}}\right) \\ $$$$=\left(\mathrm{2}\boldsymbol{{x}}−\mathrm{5}\boldsymbol{{y}}\right)\left(\mathrm{3}\boldsymbol{{x}}+\mathrm{2}\boldsymbol{{y}}\right) \\ $$
