Question Number 73396 by mathmax by abdo last updated on 11/Nov/19
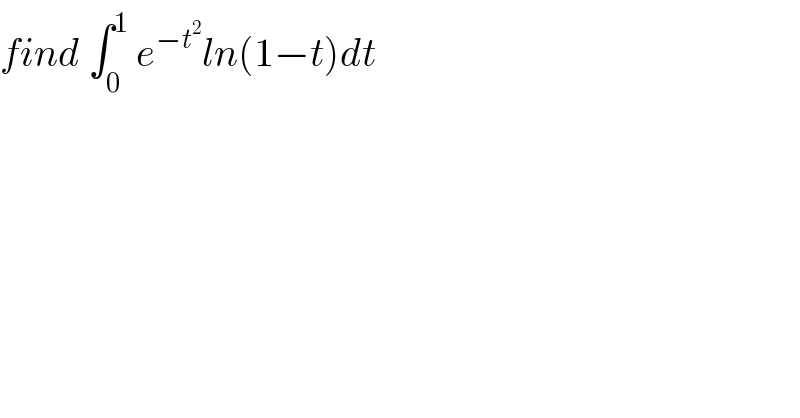
$${find}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{−{t}^{\mathrm{2}} } {ln}\left(\mathrm{1}−{t}\right){dt} \\ $$
Commented by mathmax by abdo last updated on 14/Nov/19
![let take a try let I =∫_0 ^1 e^(−t^2 ) ln(1−t)dt we have ln^′ (1−t) =((−1)/(1−t)) =−Σ_(n=0) ^∞ t^n for ∣t∣<1 ⇒ ln(1−t) =−Σ_(n=0) ^∞ (t^(n+1) /(n+1)) +c (c=0) =−Σ_(n=1) ^∞ (t^n /n) ⇒I =−∫_0 ^1 e^(−t^2 ) (Σ_(n=1) ^∞ (t^n /n))dt =−Σ_(n=1) ^∞ (1/n)∫_0 ^1 t^n e^(−t^2 ) dt =−Σ_(n=1) ^∞ (W_n /n) with W_n =∫_0 ^1 t^n e^(−t^2 ) dt by parts u^′ =t^n and v=e^(−t^2 ) ⇒ W_n =[(1/(n+1))t^(n+1) e^(−t^2 ) ]_0 ^1 −∫_0 ^1 (1/(n+1))t^(n+1) (−2t)e^(−t^2 ) dt =(e^(−1) /(n+1)) +(2/(n+1)) ∫_0 ^1 t^(n+2) e^(−t^2 ) dt =(e^(−1) /(n+1)) +(2/(n+1)) W_(n+2) ⇒ (n+1)W_n =e^(−1) +2 W_(n+2) ⇒W_(n+2) =(1/2){ (n+1)W_n −e^(−1) } ....be continued....](https://www.tinkutara.com/question/Q73699.png)
$${let}\:{take}\:{a}\:{try}\:\:{let}\:{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{−{t}^{\mathrm{2}} } {ln}\left(\mathrm{1}−{t}\right){dt}\:\:{we}\:{have} \\ $$$${ln}^{'} \left(\mathrm{1}−{t}\right)\:=\frac{−\mathrm{1}}{\mathrm{1}−{t}}\:=−\sum_{{n}=\mathrm{0}} ^{\infty} \:{t}^{{n}} \:\:\:{for}\:\mid{t}\mid<\mathrm{1}\:\Rightarrow \\ $$$${ln}\left(\mathrm{1}−{t}\right)\:=−\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{t}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\:\:\:+{c}\:\:\:\:\left({c}=\mathrm{0}\right) \\ $$$$=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{t}^{{n}} }{{n}}\:\Rightarrow{I}\:=−\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{−{t}^{\mathrm{2}} } \left(\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{t}^{{n}} }{{n}}\right){dt} \\ $$$$=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{t}^{{n}} {e}^{−{t}^{\mathrm{2}} \:} \:\:{dt}\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{{W}_{{n}} }{{n}}\:\:{with} \\ $$$${W}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{{n}} \:{e}^{−{t}^{\mathrm{2}} } \:{dt}\:\:\:{by}\:{parts}\:{u}^{'} ={t}^{{n}} \:{and}\:{v}={e}^{−{t}^{\mathrm{2}} } \:\Rightarrow \\ $$$${W}_{{n}} =\left[\frac{\mathrm{1}}{{n}+\mathrm{1}}{t}^{{n}+\mathrm{1}} \:{e}^{−{t}^{\mathrm{2}} } \right]_{\mathrm{0}} ^{\mathrm{1}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}}{{n}+\mathrm{1}}{t}^{{n}+\mathrm{1}} \left(−\mathrm{2}{t}\right){e}^{−{t}^{\mathrm{2}} } {dt} \\ $$$$=\frac{{e}^{−\mathrm{1}} }{{n}+\mathrm{1}}\:+\frac{\mathrm{2}}{{n}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{t}^{{n}+\mathrm{2}} \:{e}^{−{t}^{\mathrm{2}} } {dt}\:=\frac{{e}^{−\mathrm{1}} }{{n}+\mathrm{1}}\:+\frac{\mathrm{2}}{{n}+\mathrm{1}}\:{W}_{{n}+\mathrm{2}} \:\Rightarrow \\ $$$$\left({n}+\mathrm{1}\right){W}_{{n}} ={e}^{−\mathrm{1}} \:+\mathrm{2}\:{W}_{{n}+\mathrm{2}} \:\Rightarrow{W}_{{n}+\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\left({n}+\mathrm{1}\right){W}_{{n}} −{e}^{−\mathrm{1}} \right\} \\ $$$$….{be}\:{continued}…. \\ $$
Answered by mind is power last updated on 11/Nov/19
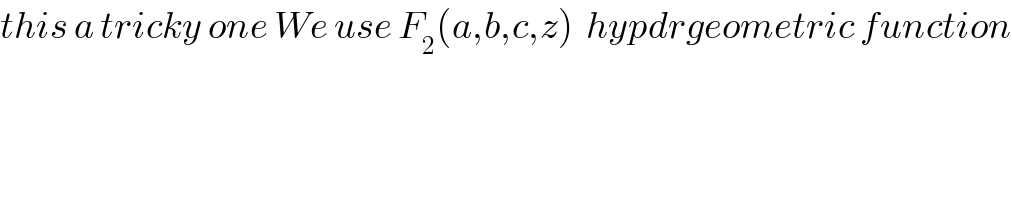
$${this}\:{a}\:{tricky}\:{one}\:{We}\:{use}\:{F}_{\mathrm{2}} \left({a},{b},{c},{z}\right)\:\:{hypdrgeometric}\:{function} \\ $$
