Question Number 76781 by mathmax by abdo last updated on 30/Dec/19
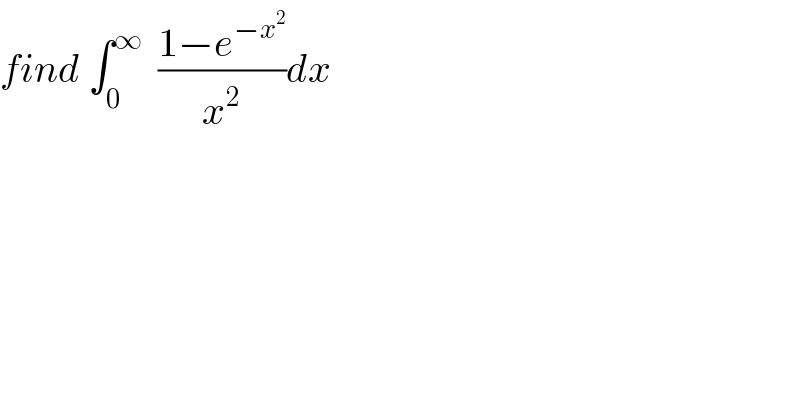
$${find}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}−{e}^{−{x}^{\mathrm{2}} } }{{x}^{\mathrm{2}} }{dx} \\ $$
Commented by ~blr237~ last updated on 30/Dec/19
![let consider f(t)=∫_0 ^∞ ((1−e^(−tx^2 ) )/x^2 )dx if t≥0 f(t) exist cause the function x→((1−e^(−tx^2 ) )/x^2 ) is continuous on [0,∞[ with an extension in 0 due to lim_(x→0) ((1−e^(−tx^2 ) )/x^2 ) = t . so Df=R_+ let a>0,b>0 and (x,t)∈D_(a,b) =[0,∞[×[a,b] ∣e^(−tx^2 ) ∣≤ e^(−ax^2 ) we know that ∫_0 ^∞ e^(−ax^2 ) dx converges cause a>0 so (x,t)→(∂/∂t)(((1−e^(−tx^2 ) )/x^2 ))verify the convergence hypothesis on D_(a,b) then f ∈C^1 ([a,b],R) ∀ a>0 b>0 finally f ∈ C^1 (R_+ ,R) we can write f′(t)=∫_0 ^∞ e^(−tx^2 ) dx= ∫_0 ^∞ e^(−(x(√t) )^2 ) ((d(x(√t) ))/( (√t))) = (1/( (√t))) ∫_0 ^∞ e^(−u^2 ) du = (√(π/(2t))) then f(t)= (√(2πt )) +c we know that f(0)=0=c ( remember that 0∈Df ) Finally f(t)=∫_0 ^∞ ((1−e^(−tx^2 ) )/x^2 )dx=(√(2πt)) the result is f(1)=∫_0 ^∞ ((1−e^(−x^2 ) )/x^2 )dx=(√(2π))](https://www.tinkutara.com/question/Q76803.png)
$$\mathrm{let}\:\mathrm{consider}\:\:\mathrm{f}\left(\mathrm{t}\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}−\mathrm{e}^{−\mathrm{tx}^{\mathrm{2}} } }{\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$\mathrm{if}\:\mathrm{t}\geqslant\mathrm{0}\:\:\:\:\mathrm{f}\left(\mathrm{t}\right)\:\:\mathrm{exist}\:\:\mathrm{cause}\:\:\mathrm{the}\:\mathrm{function} \\ $$$$\mathrm{x}\rightarrow\frac{\mathrm{1}−\mathrm{e}^{−\mathrm{tx}^{\mathrm{2}} } }{\mathrm{x}^{\mathrm{2}} }\:\mathrm{is}\:\:\mathrm{continuous}\:\mathrm{on}\:\left[\mathrm{0},\infty\left[\:\mathrm{with}\:\mathrm{an}\:\mathrm{extension}\:\mathrm{in}\:\mathrm{0}\:\mathrm{due}\:\mathrm{to}\:\right.\right. \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{e}^{−\mathrm{tx}^{\mathrm{2}} } }{\mathrm{x}^{\mathrm{2}} }\:=\:\mathrm{t}\:\:\:\:.\:\mathrm{so}\:\mathrm{Df}=\mathbb{R}_{+} \\ $$$$\mathrm{let}\:\:\mathrm{a}>\mathrm{0},\mathrm{b}>\mathrm{0}\:\:\mathrm{and}\:\left(\mathrm{x},\mathrm{t}\right)\in\mathrm{D}_{\mathrm{a},\mathrm{b}} =\left[\mathrm{0},\infty\left[×\left[\mathrm{a},\mathrm{b}\right]\right.\right. \\ $$$$\mid\mathrm{e}^{−\mathrm{tx}^{\mathrm{2}} } \mid\leqslant\:\mathrm{e}^{−\mathrm{ax}^{\mathrm{2}} } \: \\ $$$$\mathrm{we}\:\mathrm{know}\:\mathrm{that}\:\:\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{ax}^{\mathrm{2}} } \:\:\mathrm{dx}\:\mathrm{converges}\:\:\:\mathrm{cause}\:\mathrm{a}>\mathrm{0} \\ $$$$\mathrm{so}\:\:\:\:\:\left(\mathrm{x},\mathrm{t}\right)\rightarrow\frac{\partial}{\partial\mathrm{t}}\left(\frac{\mathrm{1}−\mathrm{e}^{−\mathrm{tx}^{\mathrm{2}} } }{\mathrm{x}^{\mathrm{2}} }\right)\mathrm{verify}\:\mathrm{the}\:\mathrm{convergence}\:\mathrm{hypothesis}\:\mathrm{on}\:\mathrm{D}_{\mathrm{a},\mathrm{b}} \:\mathrm{then}\:\:\mathrm{f}\:\in\mathrm{C}^{\mathrm{1}} \left(\left[\mathrm{a},\mathrm{b}\right],\mathbb{R}\right)\:\:\forall\:\mathrm{a}>\mathrm{0}\:\mathrm{b}>\mathrm{0} \\ $$$$\mathrm{finally}\:\:\mathrm{f}\:\in\:\mathrm{C}^{\mathrm{1}} \left(\mathbb{R}_{+} ,\mathbb{R}\right) \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{write}\: \\ $$$$\mathrm{f}'\left(\mathrm{t}\right)=\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{tx}^{\mathrm{2}} } \mathrm{dx}=\:\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\left(\mathrm{x}\sqrt{\mathrm{t}}\:\right)^{\mathrm{2}} } \frac{\mathrm{d}\left(\mathrm{x}\sqrt{\mathrm{t}}\:\right)}{\:\sqrt{\mathrm{t}}} \\ $$$$\:\:\:\:\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{t}}}\:\:\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{u}^{\mathrm{2}} } \mathrm{du}\:\:=\:\sqrt{\frac{\pi}{\mathrm{2t}}}\:\: \\ $$$$\mathrm{then}\:\mathrm{f}\left(\mathrm{t}\right)=\:\sqrt{\mathrm{2}\pi\mathrm{t}\:}\:+\mathrm{c}\: \\ $$$$\mathrm{we}\:\mathrm{know}\:\mathrm{that}\:\:\mathrm{f}\left(\mathrm{0}\right)=\mathrm{0}=\mathrm{c}\:\:\left(\:\mathrm{remember}\:\mathrm{that}\:\mathrm{0}\in\mathrm{Df}\:\right) \\ $$$$\mathrm{Finally}\:\:\mathrm{f}\left(\mathrm{t}\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}−\mathrm{e}^{−\mathrm{tx}^{\mathrm{2}} } }{\mathrm{x}^{\mathrm{2}} }\mathrm{dx}=\sqrt{\mathrm{2}\pi\mathrm{t}}\: \\ $$$$\mathrm{the}\:\mathrm{result}\:\mathrm{is}\:\:\mathrm{f}\left(\mathrm{1}\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}−\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } }{\mathrm{x}^{\mathrm{2}} }\mathrm{dx}=\sqrt{\mathrm{2}\pi}\: \\ $$
Commented by mathmax by abdo last updated on 10/Jan/20

$${thanks}\:{sir}. \\ $$
