Question Number 78270 by msup trace by abdo last updated on 15/Jan/20
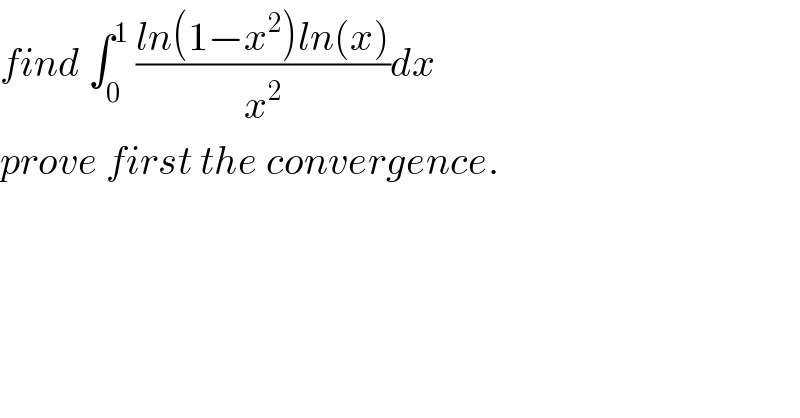
$${find}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right){ln}\left({x}\right)}{{x}^{\mathrm{2}} }{dx} \\ $$$${prove}\:{first}\:{the}\:{convergence}. \\ $$
Commented by mathmax by abdo last updated on 15/Jan/20
![let I =∫_0 ^1 ((ln(1−x^2 )ln(x))/x^2 )dx the convergence is assured by sir <mind is power> we have ln^′ (1−u)=−(1/(1−u))=−Σ_(n=0) ^∞ u^n for ∣u∣<1 ⇒ln(1−u) =−Σ_(n=0) ^∞ (u^(n+1) /(n+1)) +c (c=0)=−Σ_(n=1) ^∞ (u^n /n) ⇒ ln(1−x^2 ) =−Σ_(n=1) ^∞ (x^(2n) /n) ⇒ ((ln(1−x^2 )ln(x))/x^2 )=−Σ_(n=1) ^∞ (x^(2n−2) /n)ln(x) ⇒I =−Σ_(n=1) ^∞ (1/n) ∫_0 ^1 x^(2n−2) ln(x)dx by parts ∫_0 ^1 x^(2n−2) ln(x)dx =[(1/(2n−1))x^(2n−1) ln(x)]_0 ^1 −∫_0 ^1 (1/(2n−1))x^(2n−1) (dx/x) =−(1/(2n−1))∫_0 ^1 x^(2n−2) dx =−(1/((2n−1)^2 ))[x^(2n−1) ]_0 ^1 =((−1)/((2n−1)^2 )) ⇒ I =Σ_(n=1) ^∞ (1/(n(2n−1)^2 )) let decompose F(x)=(1/(x(2x−1)^2 )) F(x)=(a/x) +(b/(2x−1)) +(c/((2x−1)^2 )) a=xF(x)∣_(x=0) =1 c =(2x−1)^2 F(x)∣_(x=(1/2)) =2 ⇒F(x)=(1/x) +(b/(2x−1)) +(2/((2x−1)^2 )) F(1)=1 =1 +b +2 ⇒b=−2 ⇒F(x)=(1/x)−(2/(2x−1)) +(2/((2x−1)^2 )) ⇒ I =Σ_(n=1) ^∞ F(n) =Σ_(n=1) ^∞ ((1/n)−(2/(2n−1))) +2Σ_(n=1) ^∞ (1/((2n−1)^2 )) Σ_(n=1) ^∞ ((1/n)−(2/(2n−1))) =lim s_n with s_n =Σ_(k=1) ^n ((1/k)−(2/(2k−1))) =H_n −2Σ_(k=1) ^n (1/(2k−1)) but Σ_(k=1) ^n (1/(2k−1)) =1 +(1/3) +(1/5) +...+(1/(2n−1)) =1+(1/2) +(1/3) +(1/4) +... +(1/(2n−1)) +(1/(2n)) −(1/2)−(1/4)−...−(1/(2n)) =H_(2n) −(1/2) H_n ⇒ s_n =H_n −2{H_(2n) −(1/2) H_n } =2H_n −2H_(2n) =2( ln(n)+γ +o((1/n))−ln(2n)−γ+o((1/n))) =2( ln((n/(2n))) +o((1/n))) ⇒lim s_n =−2ln(2) let findA= Σ_(n=1) ^∞ (1/((2n−1)^2 )) A =Σ_(n=0) ^∞ (1/((2n+1)^2 )) we have (π^2 /6) =Σ_(n=1) ^∞ (1/n^2 ) =(1/4)Σ_(n=1) ^∞ (1/n^2 ) +Σ_(n=0) ^∞ (1/((2n+1)^2 )) ⇒ Σ_(n=0) ^∞ (1/((2n+1)^2 )) =(1−(1/4))(π^2 /6) =(3/4)×(π^2 /6) =(π^2 /8) ⇒ I =−2ln(2)+2×(π^2 /8) =(π^2 /4)−2ln(2)](https://www.tinkutara.com/question/Q78310.png)
$${let}\:{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right){ln}\left({x}\right)}{{x}^{\mathrm{2}} }{dx}\:\:\:{the}\:{convergence}\:{is}\:{assured}\:{by}\:{sir} \\ $$$$<{mind}\:{is}\:{power}>\:\:\:{we}\:{have}\:{ln}^{'} \left(\mathrm{1}−{u}\right)=−\frac{\mathrm{1}}{\mathrm{1}−{u}}=−\sum_{{n}=\mathrm{0}} ^{\infty} \:{u}^{{n}} \:\:{for} \\ $$$$\mid{u}\mid<\mathrm{1}\:\Rightarrow{ln}\left(\mathrm{1}−{u}\right)\:=−\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{u}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\:\:+{c}\:\:\left({c}=\mathrm{0}\right)=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{u}^{{n}} }{{n}}\:\Rightarrow \\ $$$${ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{\mathrm{2}{n}} }{{n}}\:\Rightarrow\:\frac{{ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right){ln}\left({x}\right)}{{x}^{\mathrm{2}} }=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{\mathrm{2}{n}−\mathrm{2}} }{{n}}{ln}\left({x}\right) \\ $$$$\Rightarrow{I}\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{{n}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{\mathrm{2}{n}−\mathrm{2}} \:{ln}\left({x}\right){dx}\:\:{by}\:{parts} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{\mathrm{2}{n}−\mathrm{2}} {ln}\left({x}\right){dx}\:=\left[\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}}{x}^{\mathrm{2}{n}−\mathrm{1}} {ln}\left({x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}}{x}^{\mathrm{2}{n}−\mathrm{1}} \frac{{dx}}{{x}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{x}^{\mathrm{2}{n}−\mathrm{2}} \:{dx}\:=−\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} }\left[{x}^{\mathrm{2}{n}−\mathrm{1}} \right]_{\mathrm{0}} ^{\mathrm{1}} \:=\frac{−\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$${I}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{{n}\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} }\:\:{let}\:{decompose}\:{F}\left({x}\right)=\frac{\mathrm{1}}{{x}\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${F}\left({x}\right)=\frac{{a}}{{x}}\:+\frac{{b}}{\mathrm{2}{x}−\mathrm{1}}\:+\frac{{c}}{\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${a}={xF}\left({x}\right)\mid_{{x}=\mathrm{0}} \:\:=\mathrm{1} \\ $$$${c}\:=\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{2}} {F}\left({x}\right)\mid_{{x}=\frac{\mathrm{1}}{\mathrm{2}}} \:\:\:=\mathrm{2}\:\Rightarrow{F}\left({x}\right)=\frac{\mathrm{1}}{{x}}\:+\frac{{b}}{\mathrm{2}{x}−\mathrm{1}}\:+\frac{\mathrm{2}}{\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${F}\left(\mathrm{1}\right)=\mathrm{1}\:=\mathrm{1}\:+{b}\:+\mathrm{2}\:\Rightarrow{b}=−\mathrm{2}\:\Rightarrow{F}\left({x}\right)=\frac{\mathrm{1}}{{x}}−\frac{\mathrm{2}}{\mathrm{2}{x}−\mathrm{1}}\:+\frac{\mathrm{2}}{\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$${I}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:{F}\left({n}\right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{2}}{\mathrm{2}{n}−\mathrm{1}}\right)\:+\mathrm{2}\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{2}}{\mathrm{2}{n}−\mathrm{1}}\right)\:={lim}\:{s}_{{n}} \:\:{with}\:{s}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \left(\frac{\mathrm{1}}{{k}}−\frac{\mathrm{2}}{\mathrm{2}{k}−\mathrm{1}}\right) \\ $$$$={H}_{{n}} −\mathrm{2}\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}\:{but} \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}\:=\mathrm{1}\:+\frac{\mathrm{1}}{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{5}}\:+…+\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}} \\ $$$$=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{4}}\:+…\:+\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{2}{n}}\:−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}−…−\frac{\mathrm{1}}{\mathrm{2}{n}} \\ $$$$={H}_{\mathrm{2}{n}} −\frac{\mathrm{1}}{\mathrm{2}}\:{H}_{{n}} \:\Rightarrow\:{s}_{{n}} ={H}_{{n}} −\mathrm{2}\left\{{H}_{\mathrm{2}{n}} −\frac{\mathrm{1}}{\mathrm{2}}\:{H}_{{n}} \right\} \\ $$$$=\mathrm{2}{H}_{{n}} −\mathrm{2}{H}_{\mathrm{2}{n}} \:\:=\mathrm{2}\left(\:{ln}\left({n}\right)+\gamma\:+{o}\left(\frac{\mathrm{1}}{{n}}\right)−{ln}\left(\mathrm{2}{n}\right)−\gamma+{o}\left(\frac{\mathrm{1}}{{n}}\right)\right) \\ $$$$=\mathrm{2}\left(\:{ln}\left(\frac{{n}}{\mathrm{2}{n}}\right)\:+{o}\left(\frac{\mathrm{1}}{{n}}\right)\right)\:\Rightarrow{lim}\:{s}_{{n}} =−\mathrm{2}{ln}\left(\mathrm{2}\right)\:{let}\:{findA}=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${A}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:{we}\:{have}\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{4}}\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:+\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:=\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}\right)\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:=\frac{\mathrm{3}}{\mathrm{4}}×\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:\Rightarrow \\ $$$${I}\:=−\mathrm{2}{ln}\left(\mathrm{2}\right)+\mathrm{2}×\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{4}}−\mathrm{2}{ln}\left(\mathrm{2}\right) \\ $$$$ \\ $$$$ \\ $$
Answered by mind is power last updated on 15/Jan/20
![cv in zero ((ln(1−x^2 ))/x^2 )∼1 ((ln(1−x^2 ))/x^2 ).ln(x)∼ln(x) log is integrabl in zero in 1 ((ln(1−x^2 ).ln(x))/x^2 )=g(x) lim_(x→1) (√(1−x )) g(x)=0⇒g(x)=o((1/( (√(1−x))))) since (1/( (√(1−x)))) is integral in 1^− ⇒g also since g is continus ]0,1[ ⇒is integrable ∫_0 ^1 ((ln(1−x^2 )ln(x))/x^2 )dx ln(1−x^2 )=−Σ_(k≥1) (x^(2k) /k) =−∫_0 ^1 Σ_(k≥1) ((x^(2k) ln(x))/k)dx =−Σ_(k≥1) ∫_0 ^1 ((ln(x)x^(2k) )/k)dx u=−ln(x)⇒dx=−e^(−u) du =Σ_(k≥1) ∫_0 ^(+∞) (((−u).(−e^(−u) )e^(−2ku) )/k)du =Σ_(k≥1) ∫_0 ^(+∞) ((ue^(−(1+2k)u) )/k)du,w=(1+2k)u⇒du=(dw/(1+2k)) =Σ_(k≥1) ∫_0 ^(+∞) ((we^(−w) )/(k(1+2k)^2 ))dw =Σ_(k≥1) (1/(k(1+2k)^2 )).∫_0 ^(+∞) we^(−w) dw=Σ_(k≥1) (1/(k(1+2k)^2 )) =Σ((1/k)−(2/((1+2k)^2 ))−(2/((1+2k)))) =Σ_(k≥1) ((2/(2k))−(2/(1+2k)))−2Σ_(k≥1) (1/((1+2k)^2 )) =2{Σ_(k≥1) (((−1)^k )/k)+1}−2((3ζ(2))/4) =2{1−ln(2))−(3/2).(π^2 /6) =2−2ln(2)−(π^2 /4)](https://www.tinkutara.com/question/Q78292.png)
$$\mathrm{cv}\: \\ $$$$\mathrm{in}\:\mathrm{zero}\: \\ $$$$\frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{x}^{\mathrm{2}} }\sim\mathrm{1} \\ $$$$\frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{x}^{\mathrm{2}} }.\mathrm{ln}\left(\mathrm{x}\right)\sim\mathrm{ln}\left(\mathrm{x}\right)\:\:\mathrm{log}\:\mathrm{is}\:\mathrm{integrabl}\:\mathrm{in}\:\mathrm{zero} \\ $$$$\mathrm{in}\:\mathrm{1} \\ $$$$\frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right).\mathrm{ln}\left(\mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} }=\mathrm{g}\left(\mathrm{x}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\sqrt{\mathrm{1}−\mathrm{x}\:}\:\mathrm{g}\left(\mathrm{x}\right)=\mathrm{0}\Rightarrow\mathrm{g}\left(\mathrm{x}\right)=\mathrm{o}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\mathrm{x}}}\right) \\ $$$$\mathrm{since}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\mathrm{x}}}\:\mathrm{is}\:\mathrm{integral}\:\mathrm{in}\:\mathrm{1}^{−} \Rightarrow\mathrm{g}\:\mathrm{also} \\ $$$$\left.\mathrm{since}\:\mathrm{g}\:\mathrm{is}\:\mathrm{continus}\:\right]\mathrm{0},\mathrm{1}\left[\:\Rightarrow\mathrm{is}\:\mathrm{integrable}\right. \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)\mathrm{ln}\left(\mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$\mathrm{ln}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)=−\underset{\mathrm{k}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{x}^{\mathrm{2k}} }{\mathrm{k}} \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \underset{\mathrm{k}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{x}^{\mathrm{2k}} \mathrm{ln}\left(\mathrm{x}\right)}{\mathrm{k}}\mathrm{dx} \\ $$$$=−\underset{\mathrm{k}\geqslant\mathrm{1}} {\sum}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{x}\right)\mathrm{x}^{\mathrm{2k}} }{\mathrm{k}}\mathrm{dx} \\ $$$$\mathrm{u}=−\mathrm{ln}\left(\mathrm{x}\right)\Rightarrow\mathrm{dx}=−\mathrm{e}^{−\mathrm{u}} \mathrm{du} \\ $$$$=\underset{\mathrm{k}\geqslant\mathrm{1}} {\sum}\int_{\mathrm{0}} ^{+\infty} \frac{\left(−\mathrm{u}\right).\left(−\mathrm{e}^{−\mathrm{u}} \right)\mathrm{e}^{−\mathrm{2ku}} }{\mathrm{k}}\mathrm{du} \\ $$$$=\underset{\mathrm{k}\geqslant\mathrm{1}} {\sum}\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{ue}^{−\left(\mathrm{1}+\mathrm{2k}\right)\mathrm{u}} }{\mathrm{k}}\mathrm{du},\mathrm{w}=\left(\mathrm{1}+\mathrm{2k}\right)\mathrm{u}\Rightarrow\mathrm{du}=\frac{\mathrm{dw}}{\mathrm{1}+\mathrm{2k}} \\ $$$$=\underset{\mathrm{k}\geqslant\mathrm{1}} {\sum}\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{we}^{−\mathrm{w}} }{\mathrm{k}\left(\mathrm{1}+\mathrm{2k}\right)^{\mathrm{2}} }\mathrm{dw} \\ $$$$=\underset{\mathrm{k}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\mathrm{k}\left(\mathrm{1}+\mathrm{2k}\right)^{\mathrm{2}} }.\int_{\mathrm{0}} ^{+\infty} \mathrm{we}^{−\mathrm{w}} \mathrm{dw}=\underset{\mathrm{k}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\mathrm{k}\left(\mathrm{1}+\mathrm{2k}\right)^{\mathrm{2}} } \\ $$$$=\Sigma\left(\frac{\mathrm{1}}{\mathrm{k}}−\frac{\mathrm{2}}{\left(\mathrm{1}+\mathrm{2k}\right)^{\mathrm{2}} }−\frac{\mathrm{2}}{\left(\mathrm{1}+\mathrm{2k}\right)}\right) \\ $$$$=\underset{\mathrm{k}\geqslant\mathrm{1}} {\sum}\left(\frac{\mathrm{2}}{\mathrm{2k}}−\frac{\mathrm{2}}{\mathrm{1}+\mathrm{2k}}\right)−\mathrm{2}\underset{\mathrm{k}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{2k}\right)^{\mathrm{2}} } \\ $$$$=\mathrm{2}\left\{\underset{\mathrm{k}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\mathrm{k}}+\mathrm{1}\right\}−\mathrm{2}\frac{\mathrm{3}\zeta\left(\mathrm{2}\right)}{\mathrm{4}} \\ $$$$=\mathrm{2}\left\{\mathrm{1}−\mathrm{ln}\left(\mathrm{2}\right)\right)−\frac{\mathrm{3}}{\mathrm{2}}.\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$=\mathrm{2}−\mathrm{2ln}\left(\mathrm{2}\right)−\frac{\pi^{\mathrm{2}} }{\mathrm{4}} \\ $$
Commented by msup trace by abdo last updated on 15/Jan/20

$${thank}\:{you}\:{sir}. \\ $$
Commented by mind is power last updated on 15/Jan/20

$$\mathrm{y}'\mathrm{re}\:\mathrm{Welcom} \\ $$
