Question Number 73478 by abdomathmax last updated on 13/Nov/19
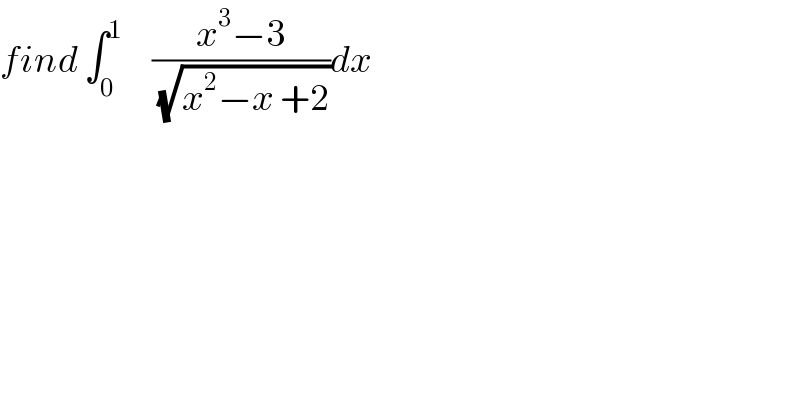
$${find}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\:\frac{{x}^{\mathrm{3}} −\mathrm{3}}{\:\sqrt{{x}^{\mathrm{2}} −{x}\:+\mathrm{2}}}{dx} \\ $$
Answered by MJS last updated on 13/Nov/19
![∫((x^3 −3)/( (√(x^3 −x+2))))dx=∫((x^3 −3)/( (√((x−(1/2))^2 +(7/4)))))dx= [t=((2x−1)/( (√7))) → dx=((√7)/2)dt] =(1/8)∫((7(√7)t^3 +21t^2 +3(√7)t−23)/( (√(t^2 +1))))dt= [t=sinh ln u =((u^2 −1)/(2u)) ⇒ u=t+(√(t^2 +1)) → dt=((√(t^2 +1))/(t+(√(t^2 +1))))du=((u^2 +1)/(2u^2 ))du] =(1/(64))∫((7(√7)u^6 +42u^5 −9(√7)u^4 −268u^3 +9(√7)u^2 +42u−7(√7))/u^4 )du and it′s easy to solve this](https://www.tinkutara.com/question/Q73515.png)
$$\int\frac{{x}^{\mathrm{3}} −\mathrm{3}}{\:\sqrt{{x}^{\mathrm{3}} −{x}+\mathrm{2}}}{dx}=\int\frac{{x}^{\mathrm{3}} −\mathrm{3}}{\:\sqrt{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{7}}{\mathrm{4}}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{7}}}\:\rightarrow\:{dx}=\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}{dt}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\int\frac{\mathrm{7}\sqrt{\mathrm{7}}{t}^{\mathrm{3}} +\mathrm{21}{t}^{\mathrm{2}} +\mathrm{3}\sqrt{\mathrm{7}}{t}−\mathrm{23}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}{dt}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{sinh}\:\mathrm{ln}\:{u}\:=\frac{{u}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{u}}\:\Rightarrow\:{u}={t}+\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}\:\rightarrow\:{dt}=\frac{\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}{{t}+\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}{du}=\frac{{u}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{u}^{\mathrm{2}} }{du}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{64}}\int\frac{\mathrm{7}\sqrt{\mathrm{7}}{u}^{\mathrm{6}} +\mathrm{42}{u}^{\mathrm{5}} −\mathrm{9}\sqrt{\mathrm{7}}{u}^{\mathrm{4}} −\mathrm{268}{u}^{\mathrm{3}} +\mathrm{9}\sqrt{\mathrm{7}}{u}^{\mathrm{2}} +\mathrm{42}{u}−\mathrm{7}\sqrt{\mathrm{7}}}{{u}^{\mathrm{4}} }{du} \\ $$$$\mathrm{and}\:\mathrm{it}'\mathrm{s}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{this} \\ $$
Commented by abdomathmax last updated on 17/Nov/19

$${thank}\:{you}\:{sir}. \\ $$
