Menu Close

find-0-1-x-n-ln-1-x-4-dx-with-n-integr-natural-

Tinku Tara 0 Comments
Pin




Question Number 135382 by Bird last updated on 12/Mar/21
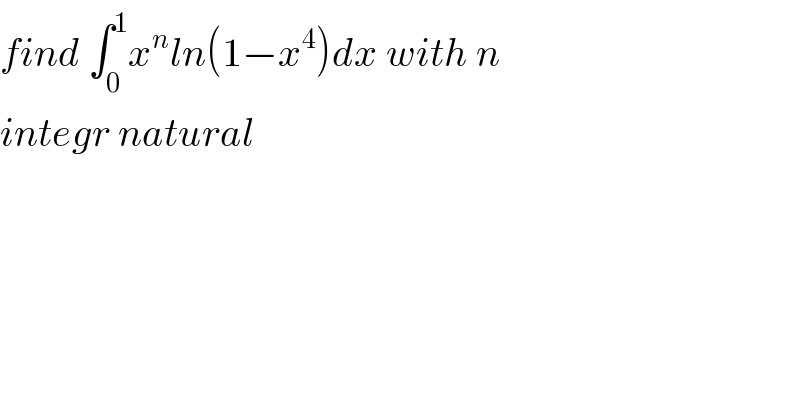
find ∫_0 ^1 x^n ln(1−x^4 )dx with n integr natural
$${find}\:\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} {ln}\left(\mathrm{1}−{x}^{\mathrm{4}} \right){dx}\:{with}\:{n} \\ $$$${integr}\:{natural} \\ $$
Answered by Dwaipayan Shikari last updated on 12/Mar/21
x^4 =t =(1/4)∫_0 ^1 t^((n/4)−(3/4)) log(1−t)dt I(a,b)=∫_0 ^1 t^(a−1) (1−t)^(b−1) dt=((Γ(a)Γ(b))/(Γ(a+b))) (∂/∂b)I(a,b)=∫_0 ^1 t^(a−1) (1−t)^(b−1) log(1−t)=((Γ(a+b)Γ′(b)Γ(a)−Γ′(a+b)Γ(a)Γ(b)))/(Γ^2 (a+b))) =((Γ(a)Γ(b))/(Γ(a+b)))(ψ(b)−ψ(a+b)) b=1 a=((n+1)/4) (1/4)I(((n+1)/4),1)=(1/4)∫_0 ^1 t^((n/4)−(3/4)) log(1−t)dt=((Γ(((n+1)/4)))/(Γ(n+(1/4)+1)))(−γ−ψ(((n+5)/4))) =−(4/(4n+1))(γ+ψ(((n+5)/4)))
$${x}^{\mathrm{4}} ={t} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\frac{{n}}{\mathrm{4}}−\frac{\mathrm{3}}{\mathrm{4}}} {log}\left(\mathrm{1}−{t}\right){dt} \\ $$$${I}\left({a},{b}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{a}−\mathrm{1}} \left(\mathrm{1}−{t}\right)^{{b}−\mathrm{1}} {dt}=\frac{\Gamma\left({a}\right)\Gamma\left({b}\right)}{\Gamma\left({a}+{b}\right)} \\ $$$$\frac{\partial}{\partial{b}}{I}\left({a},{b}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{a}−\mathrm{1}} \left(\mathrm{1}−{t}\right)^{{b}−\mathrm{1}} {log}\left(\mathrm{1}−{t}\right)=\frac{\left.\Gamma\left({a}+{b}\right)\Gamma'\left({b}\right)\Gamma\left({a}\right)−\Gamma'\left({a}+{b}\right)\Gamma\left({a}\right)\Gamma\left({b}\right)\right)}{\Gamma^{\mathrm{2}} \left({a}+{b}\right)} \\ $$$$=\frac{\Gamma\left({a}\right)\Gamma\left({b}\right)}{\Gamma\left({a}+{b}\right)}\left(\psi\left({b}\right)−\psi\left({a}+{b}\right)\right) \\ $$$${b}=\mathrm{1} \\ $$$${a}=\frac{{n}+\mathrm{1}}{\mathrm{4}} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}{I}\left(\frac{{n}+\mathrm{1}}{\mathrm{4}},\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\frac{{n}}{\mathrm{4}}−\frac{\mathrm{3}}{\mathrm{4}}} {log}\left(\mathrm{1}−{t}\right){dt}=\frac{\Gamma\left(\frac{{n}+\mathrm{1}}{\mathrm{4}}\right)}{\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{1}\right)}\left(−\gamma−\psi\left(\frac{{n}+\mathrm{5}}{\mathrm{4}}\right)\right) \\ $$$$=−\frac{\mathrm{4}}{\mathrm{4}{n}+\mathrm{1}}\left(\gamma+\psi\left(\frac{{n}+\mathrm{5}}{\mathrm{4}}\right)\right) \\ $$
Commented by mathmax by abdo last updated on 12/Mar/21
thank you sir
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *