Question Number 137055 by mathmax by abdo last updated on 29/Mar/21
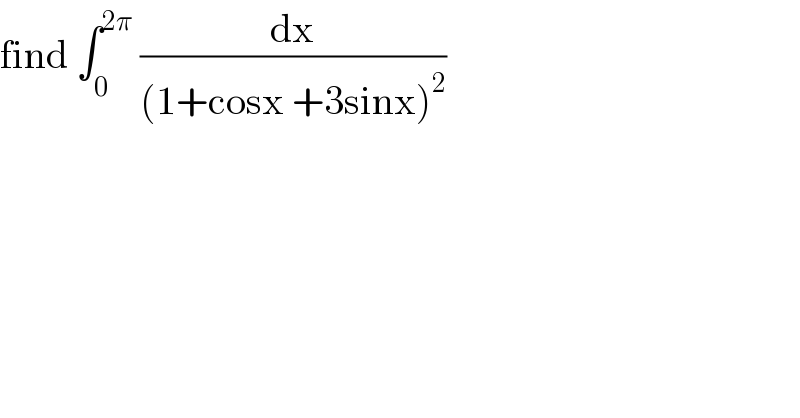
$$\mathrm{find}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{\mathrm{dx}}{\left(\mathrm{1}+\mathrm{cosx}\:+\mathrm{3sinx}\right)^{\mathrm{2}} } \\ $$
Commented by MJS_new last updated on 30/Mar/21
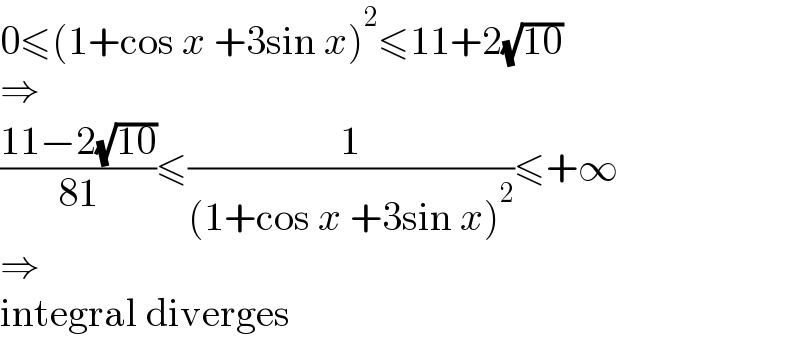
$$\mathrm{0}\leqslant\left(\mathrm{1}+\mathrm{cos}\:{x}\:+\mathrm{3sin}\:{x}\right)^{\mathrm{2}} \leqslant\mathrm{11}+\mathrm{2}\sqrt{\mathrm{10}} \\ $$$$\Rightarrow \\ $$$$\frac{\mathrm{11}−\mathrm{2}\sqrt{\mathrm{10}}}{\mathrm{81}}\leqslant\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{cos}\:{x}\:+\mathrm{3sin}\:{x}\right)^{\mathrm{2}} }\leqslant+\infty \\ $$$$\Rightarrow \\ $$$$\mathrm{integral}\:\mathrm{diverges} \\ $$
Answered by Dwaipayan Shikari last updated on 30/Mar/21
![∫_0 ^(2π) (dx/((2cos^2 (x/2)+6sin(x/2)cos(x/2)))) =(1/4)∫((sec^2 (x/2))/((cos(x/2)+3sin(x/2))^2 ))dx=(1/4)∫((sec^4 (x/2))/((1+3tan(x/2))^2 ))dx =(1/2)∫((sec^4 u)/((1+3tanu)^2 ))du=(1/2)∫(((1+t^2 ))/((1+3t)^2 ))dt =(1/(18))∫(dt/((t+(1/3))^2 ))+(1/(18))∫((t^2 +((2t)/3)+(1/9))/((t+(1/3))^2 ))−(1/(18))∫((((2t)/3)+(1/9))/((t+(1/3))^2 ))dt =−(1/(18)).(1/(t+(1/3)))+(1/(18))−(1/(27))log(t+(1/3))+(1/(162(t+(1/3))))−(1/(81(t+(1/3)))) =[(1/(tan((x/2))))((1/(162))−(1/(18))−(1/(81)))+(1/(18))−(1/(27))log(tan(x/2)+(1/3))]_0 ^(2π) Diverges](https://www.tinkutara.com/question/Q137138.png)
$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{{dx}}{\left(\mathrm{2}{cos}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}+\mathrm{6}{sin}\frac{{x}}{\mathrm{2}}{cos}\frac{{x}}{\mathrm{2}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\left({cos}\frac{{x}}{\mathrm{2}}+\mathrm{3}{sin}\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} }{dx}=\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{sec}^{\mathrm{4}} \frac{{x}}{\mathrm{2}}}{\left(\mathrm{1}+\mathrm{3}{tan}\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} }{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{sec}^{\mathrm{4}} {u}}{\left(\mathrm{1}+\mathrm{3}{tanu}\right)^{\mathrm{2}} }{du}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{\left(\mathrm{1}+\mathrm{3}{t}\right)^{\mathrm{2}} }{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{18}}\int\frac{{dt}}{\left({t}+\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{18}}\int\frac{{t}^{\mathrm{2}} +\frac{\mathrm{2}{t}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{9}}}{\left({t}+\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{18}}\int\frac{\frac{\mathrm{2}{t}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{9}}}{\left({t}+\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} }{dt} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{18}}.\frac{\mathrm{1}}{{t}+\frac{\mathrm{1}}{\mathrm{3}}}+\frac{\mathrm{1}}{\mathrm{18}}−\frac{\mathrm{1}}{\mathrm{27}}{log}\left({t}+\frac{\mathrm{1}}{\mathrm{3}}\right)+\frac{\mathrm{1}}{\mathrm{162}\left({t}+\frac{\mathrm{1}}{\mathrm{3}}\right)}−\frac{\mathrm{1}}{\mathrm{81}\left({t}+\frac{\mathrm{1}}{\mathrm{3}}\right)} \\ $$$$=\left[\frac{\mathrm{1}}{{tan}\left(\frac{{x}}{\mathrm{2}}\right)}\left(\frac{\mathrm{1}}{\mathrm{162}}−\frac{\mathrm{1}}{\mathrm{18}}−\frac{\mathrm{1}}{\mathrm{81}}\right)+\frac{\mathrm{1}}{\mathrm{18}}−\frac{\mathrm{1}}{\mathrm{27}}{log}\left({tan}\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}\right)\right]_{\mathrm{0}} ^{\mathrm{2}\pi} \\ $$$${Diverges} \\ $$
