Menu Close

find-0-e-x-3-sin-x-3-dx-

Tinku Tara 0 Comments
Pin




Question Number 66150 by mathmax by abdo last updated on 09/Aug/19
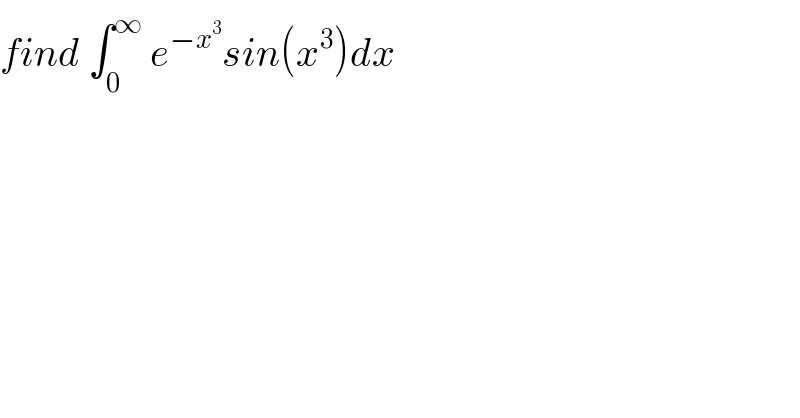
find ∫_0 ^∞ e^(−x^3 ) sin(x^3 )dx
$${find}\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{x}^{\mathrm{3}} } {sin}\left({x}^{\mathrm{3}} \right){dx}\: \\ $$
Commented by mathmax by abdo last updated on 11/Aug/19
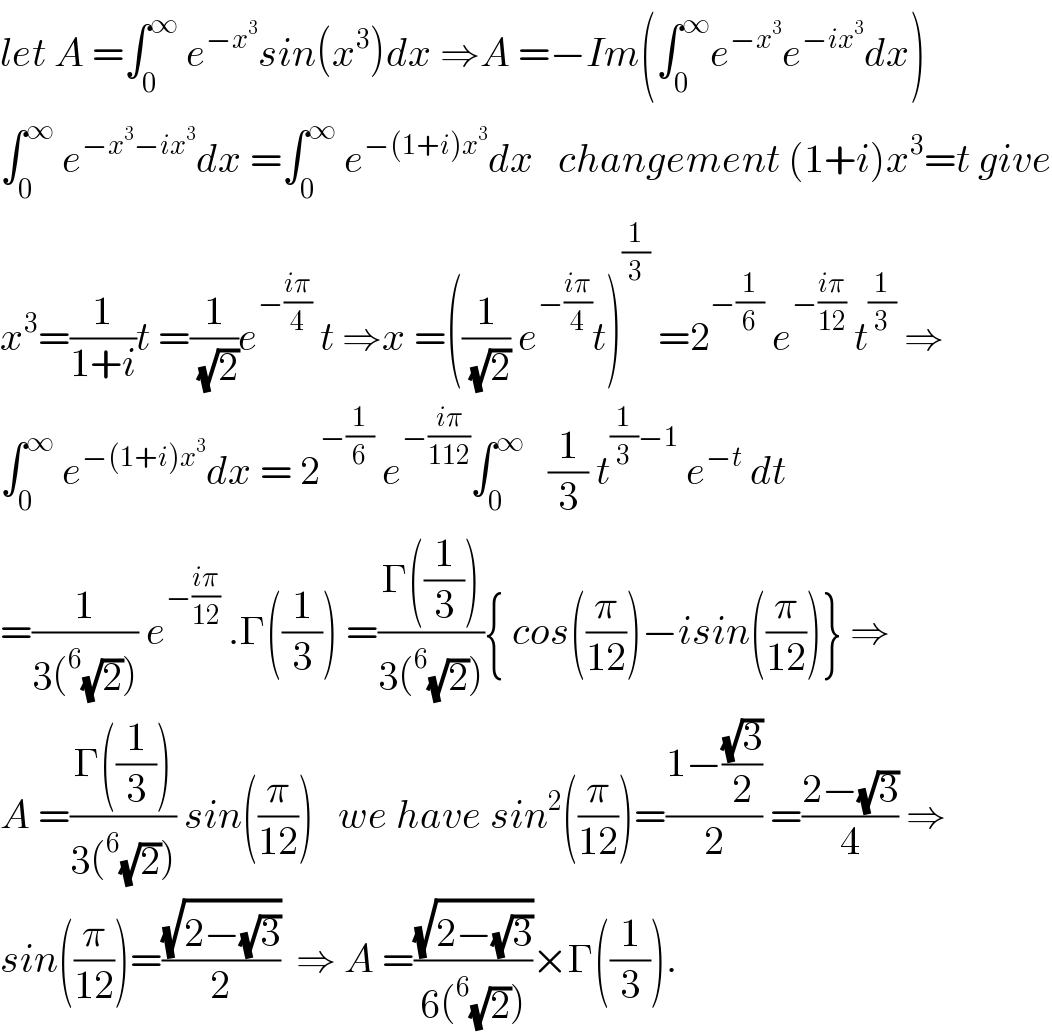
let A =∫_0 ^∞ e^(−x^3 ) sin(x^3 )dx ⇒A =−Im(∫_0 ^∞ e^(−x^3 ) e^(−ix^3 ) dx) ∫_0 ^∞ e^(−x^3 −ix^3 ) dx =∫_0 ^∞ e^(−(1+i)x^3 ) dx changement (1+i)x^3 =t give x^3 =(1/(1+i))t =(1/( (√2)))e^(−((iπ)/4)) t ⇒x =((1/( (√2))) e^(−((iπ)/4)) t)^(1/3) =2^(−(1/6)) e^(−((iπ)/(12))) t^(1/3) ⇒ ∫_0 ^∞ e^(−(1+i)x^3 ) dx = 2^(−(1/6)) e^(−((iπ)/(112))) ∫_0 ^∞ (1/3) t^((1/3)−1) e^(−t) dt =(1/(3(^6 (√2)))) e^(−((iπ)/(12))) .Γ((1/3)) =((Γ((1/3)))/(3(^6 (√2)))){ cos((π/(12)))−isin((π/(12)))} ⇒ A =((Γ((1/3)))/(3(^6 (√2)))) sin((π/(12))) we have sin^2 ((π/(12)))=((1−((√3)/2))/2) =((2−(√3))/4) ⇒ sin((π/(12)))=((√(2−(√3)))/2) ⇒ A =((√(2−(√3)))/(6(^6 (√2))))×Γ((1/3)).
$${let}\:{A}\:=\int_{\mathrm{0}} ^{\infty} \:{e}^{−{x}^{\mathrm{3}} } {sin}\left({x}^{\mathrm{3}} \right){dx}\:\Rightarrow{A}\:=−{Im}\left(\int_{\mathrm{0}} ^{\infty} {e}^{−{x}^{\mathrm{3}} } {e}^{−{ix}^{\mathrm{3}} } {dx}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{e}^{−{x}^{\mathrm{3}} −{ix}^{\mathrm{3}} } {dx}\:=\int_{\mathrm{0}} ^{\infty} \:{e}^{−\left(\mathrm{1}+{i}\right){x}^{\mathrm{3}} } {dx}\:\:\:{changement}\:\left(\mathrm{1}+{i}\right){x}^{\mathrm{3}} ={t}\:{give} \\ $$$${x}^{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{1}+{i}}{t}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:{t}\:\Rightarrow{x}\:=\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} {t}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:=\mathrm{2}^{−\frac{\mathrm{1}}{\mathrm{6}}} \:{e}^{−\frac{{i}\pi}{\mathrm{12}}} \:{t}^{\frac{\mathrm{1}}{\mathrm{3}}} \:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{e}^{−\left(\mathrm{1}+{i}\right){x}^{\mathrm{3}} } {dx}\:=\:\mathrm{2}^{−\frac{\mathrm{1}}{\mathrm{6}}} \:{e}^{−\frac{{i}\pi}{\mathrm{112}}} \int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{1}}{\mathrm{3}}\:{t}^{\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}} \:{e}^{−{t}} \:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}\left(^{\mathrm{6}} \sqrt{\mathrm{2}}\right)}\:{e}^{−\frac{{i}\pi}{\mathrm{12}}} \:.\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\:=\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right)}{\mathrm{3}\left(^{\mathrm{6}} \sqrt{\mathrm{2}}\right)}\left\{\:{cos}\left(\frac{\pi}{\mathrm{12}}\right)−{isin}\left(\frac{\pi}{\mathrm{12}}\right)\right\}\:\Rightarrow \\ $$$${A}\:=\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right)}{\mathrm{3}\left(^{\mathrm{6}} \sqrt{\mathrm{2}}\right)}\:{sin}\left(\frac{\pi}{\mathrm{12}}\right)\:\:\:{we}\:{have}\:{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{12}}\right)=\frac{\mathrm{1}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}{\mathrm{2}}\:=\frac{\mathrm{2}−\sqrt{\mathrm{3}}}{\mathrm{4}}\:\Rightarrow \\ $$$${sin}\left(\frac{\pi}{\mathrm{12}}\right)=\frac{\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}}{\mathrm{2}}\:\:\Rightarrow\:{A}\:=\frac{\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}}{\mathrm{6}\left(^{\mathrm{6}} \sqrt{\mathrm{2}}\right)}×\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right). \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *