Question Number 66346 by mathmax by abdo last updated on 12/Aug/19
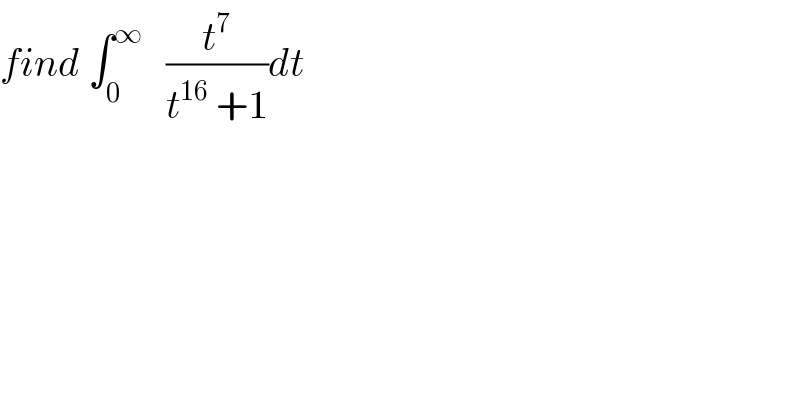
$${find}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{t}^{\mathrm{7}} }{{t}^{\mathrm{16}} \:+\mathrm{1}}{dt} \\ $$
Commented by mathmax by abdo last updated on 13/Aug/19
![let f(y) =∫_0 ^y (t^7 /(t^(16) +1))dt ⇒f(y) =(1/8)∫_0 ^y ((8t^7 )/((t^8 )^2 +1))dt =(1/8)[arctan(t^8 )]_0 ^y =(1/8) arctan(y^8 ) ⇒∫_0 ^∞ (t^7 /(t^(16) +1))dt =lim_(y→+∞) f(y) =(1/8)(π/2) =(π/(16)) another way changement t=u^(1/(16)) give ∫_0 ^∞ (t^7 /(1+t^(16) ))dt =(1/(16)) ∫_0 ^∞ (u^(7/(16)) /(1+u)) u^((1/(16))−1) du =(1/(16))∫_0 ^∞ (u^((1/2)−1) /(1+u))du =(1/(16)) (π/(sin((π/2)))) =(π/(16)) by using the result ∫_0 ^∞ (t^(a−1) /(1+t))dt =(π/(sin(πa))) ( 0<a<1)](https://www.tinkutara.com/question/Q66375.png)
$${let}\:{f}\left({y}\right)\:=\int_{\mathrm{0}} ^{{y}} \:\frac{{t}^{\mathrm{7}} }{{t}^{\mathrm{16}} \:+\mathrm{1}}{dt}\:\Rightarrow{f}\left({y}\right)\:=\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{{y}} \:\frac{\mathrm{8}{t}^{\mathrm{7}} }{\left({t}^{\mathrm{8}} \right)^{\mathrm{2}} \:+\mathrm{1}}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left[{arctan}\left({t}^{\mathrm{8}} \right)\right]_{\mathrm{0}} ^{{y}} \:=\frac{\mathrm{1}}{\mathrm{8}}\:{arctan}\left({y}^{\mathrm{8}} \right)\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\frac{{t}^{\mathrm{7}} }{{t}^{\mathrm{16}} \:+\mathrm{1}}{dt}\:={lim}_{{y}\rightarrow+\infty} {f}\left({y}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\frac{\pi}{\mathrm{2}}\:=\frac{\pi}{\mathrm{16}} \\ $$$${another}\:{way}\:\:{changement}\:{t}={u}^{\frac{\mathrm{1}}{\mathrm{16}}} \:\:{give} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{{t}^{\mathrm{7}} }{\mathrm{1}+{t}^{\mathrm{16}} }{dt}\:=\frac{\mathrm{1}}{\mathrm{16}}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{u}^{\frac{\mathrm{7}}{\mathrm{16}}} }{\mathrm{1}+{u}}\:{u}^{\frac{\mathrm{1}}{\mathrm{16}}−\mathrm{1}} {du}\:=\frac{\mathrm{1}}{\mathrm{16}}\int_{\mathrm{0}} ^{\infty} \:\frac{{u}^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} }{\mathrm{1}+{u}}{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\:\frac{\pi}{{sin}\left(\frac{\pi}{\mathrm{2}}\right)}\:=\frac{\pi}{\mathrm{16}}\:\:\:{by}\:{using}\:{the}\:{result}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{t}^{{a}−\mathrm{1}} }{\mathrm{1}+{t}}{dt}\:=\frac{\pi}{{sin}\left(\pi{a}\right)} \\ $$$$\left(\:\mathrm{0}<{a}<\mathrm{1}\right) \\ $$
Commented by Prithwish sen last updated on 13/Aug/19

$$\mathrm{nice}\:\mathrm{sir} \\ $$
