Menu Close

find-1-1-x-2-arctan-1-1-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 67374 by mathmax by abdo last updated on 26/Aug/19
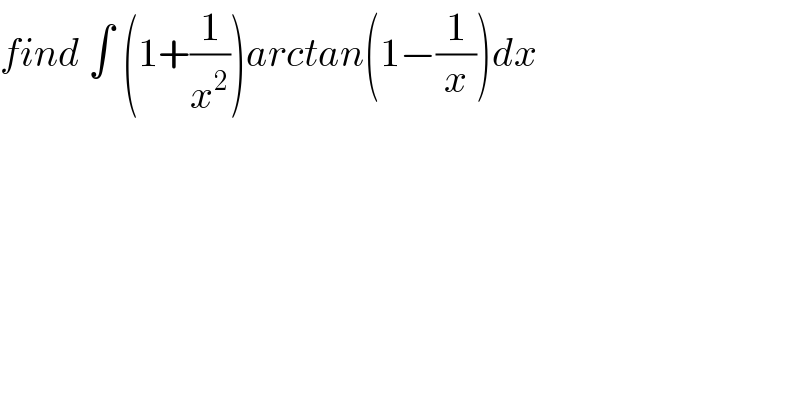
find ∫ (1+(1/x^2 ))arctan(1−(1/x))dx
$${find}\:\int\:\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right){arctan}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right){dx} \\ $$
Commented by Abdo msup. last updated on 27/Aug/19
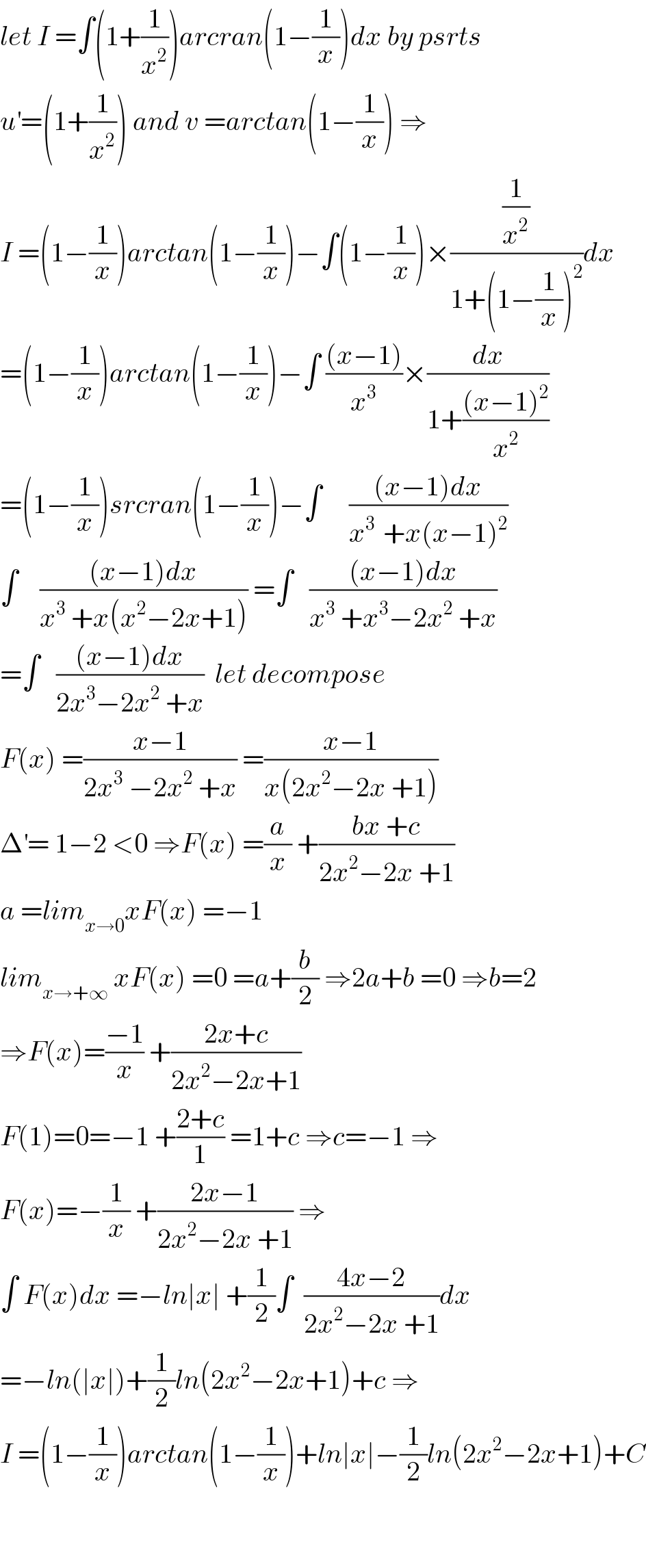
let I =∫(1+(1/x^2 ))arcran(1−(1/x))dx by psrts u^′ =(1+(1/x^2 )) and v =arctan(1−(1/x)) ⇒ I =(1−(1/x))arctan(1−(1/x))−∫(1−(1/x))×((1/x^2 )/(1+(1−(1/x))^2 ))dx =(1−(1/x))arctan(1−(1/x))−∫ (((x−1))/x^3 )×(dx/(1+(((x−1)^2 )/x^2 ))) =(1−(1/x))srcran(1−(1/x))−∫ (((x−1)dx)/(x^(3 ) +x(x−1)^2 )) ∫ (((x−1)dx)/(x^3 +x(x^2 −2x+1))) =∫ (((x−1)dx)/(x^3 +x^3 −2x^2 +x)) =∫ (((x−1)dx)/(2x^3 −2x^2 +x)) let decompose F(x) =((x−1)/(2x^3 −2x^2 +x)) =((x−1)/(x(2x^2 −2x +1))) Δ^′ = 1−2 <0 ⇒F(x) =(a/x) +((bx +c)/(2x^2 −2x +1)) a =lim_(x→0) xF(x) =−1 lim_(x→+∞) xF(x) =0 =a+(b/2) ⇒2a+b =0 ⇒b=2 ⇒F(x)=((−1)/x) +((2x+c)/(2x^2 −2x+1)) F(1)=0=−1 +((2+c)/1) =1+c ⇒c=−1 ⇒ F(x)=−(1/x) +((2x−1)/(2x^2 −2x +1)) ⇒ ∫ F(x)dx =−ln∣x∣ +(1/2)∫ ((4x−2)/(2x^2 −2x +1))dx =−ln(∣x∣)+(1/2)ln(2x^2 −2x+1)+c ⇒ I =(1−(1/x))arctan(1−(1/x))+ln∣x∣−(1/2)ln(2x^2 −2x+1)+C
$${let}\:{I}\:=\int\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right){arcran}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right){dx}\:{by}\:{psrts} \\ $$$${u}^{'} =\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)\:{and}\:{v}\:={arctan}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)\:\Rightarrow \\ $$$${I}\:=\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right){arctan}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)−\int\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)×\frac{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\mathrm{1}+\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} }{dx} \\ $$$$=\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right){arctan}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)−\int\:\frac{\left({x}−\mathrm{1}\right)}{{x}^{\mathrm{3}} }×\frac{{dx}}{\mathrm{1}+\frac{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} }} \\ $$$$=\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right){srcran}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)−\int\:\:\:\:\:\frac{\left({x}−\mathrm{1}\right){dx}}{{x}^{\mathrm{3}\:} \:+{x}\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\int\:\:\:\:\frac{\left({x}−\mathrm{1}\right){dx}}{{x}^{\mathrm{3}} \:+{x}\left({x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}\right)}\:=\int\:\:\:\frac{\left({x}−\mathrm{1}\right){dx}}{{x}^{\mathrm{3}} \:+{x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} \:+{x}} \\ $$$$=\int\:\:\:\frac{\left({x}−\mathrm{1}\right){dx}}{\mathrm{2}{x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} \:+{x}}\:\:{let}\:{decompose} \\ $$$${F}\left({x}\right)\:=\frac{{x}−\mathrm{1}}{\mathrm{2}{x}^{\mathrm{3}} \:−\mathrm{2}{x}^{\mathrm{2}} \:+{x}}\:=\frac{{x}−\mathrm{1}}{{x}\left(\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}\:+\mathrm{1}\right)} \\ $$$$\Delta^{'} =\:\mathrm{1}−\mathrm{2}\:<\mathrm{0}\:\Rightarrow{F}\left({x}\right)\:=\frac{{a}}{{x}}\:+\frac{{bx}\:+{c}}{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}\:+\mathrm{1}} \\ $$$${a}\:={lim}_{{x}\rightarrow\mathrm{0}} {xF}\left({x}\right)\:=−\mathrm{1} \\ $$$${lim}_{{x}\rightarrow+\infty} \:{xF}\left({x}\right)\:=\mathrm{0}\:={a}+\frac{{b}}{\mathrm{2}}\:\Rightarrow\mathrm{2}{a}+{b}\:=\mathrm{0}\:\Rightarrow{b}=\mathrm{2} \\ $$$$\Rightarrow{F}\left({x}\right)=\frac{−\mathrm{1}}{{x}}\:+\frac{\mathrm{2}{x}+{c}}{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}} \\ $$$${F}\left(\mathrm{1}\right)=\mathrm{0}=−\mathrm{1}\:+\frac{\mathrm{2}+{c}}{\mathrm{1}}\:=\mathrm{1}+{c}\:\Rightarrow{c}=−\mathrm{1}\:\Rightarrow \\ $$$${F}\left({x}\right)=−\frac{\mathrm{1}}{{x}}\:+\frac{\mathrm{2}{x}−\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}\:+\mathrm{1}}\:\Rightarrow \\ $$$$\int\:{F}\left({x}\right){dx}\:=−{ln}\mid{x}\mid\:+\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{\mathrm{4}{x}−\mathrm{2}}{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}\:+\mathrm{1}}{dx} \\ $$$$=−{ln}\left(\mid{x}\mid\right)+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}\right)+{c}\:\Rightarrow \\ $$$${I}\:=\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right){arctan}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)+{ln}\mid{x}\mid−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}\right)+{C} \\ $$$$ \\ $$$$ \\ $$
Commented by ~ À ® @ 237 ~ last updated on 27/Aug/19
let it be f(x) when stating u=1−(1/x) ⇔ x=(1/(1−u)) ⇒ dx=(du/((1−u)^2 )) f(x)=g(u)=∫ [(1/((1−u)^2 )) +1]arctanu du by parts A′=(1/((1−u)^2 )) +u B=arctanu ⇒ A= (1/(1−u)) + (1/2)(u^2 +1) and B′= (1/(1+u^2 )) f(x)=g(u)= [((arctanu)/(1−u)) +(1/2)(u^2 +1)arctanu]−∫ [(1/((1−u)(1+u^2 ))) +(1/2) ]du Now let find h(u)=∫ (du/((1−u)(1+u^2 ))) =(1/2) ∫ (((u^2 +1)−(u^2 −1))/((1−u)(u^2 +1))) du h(u)= (1/2) ∫ [(1/(1−u)) + ((1+u)/(1+u^2 )) ] du = (1/2)∫ (du/(1−u)) + (1/2)∫ (du/(1+u^2 )) +(1/4)∫ ((2u)/(1+u^2 )) du = ((−1)/2)ln∣1−u∣ +(1/2)arctanu +(1/4)ln∣1+u^2 ∣ + c finally knowing that u=1−(1/x) f(x)=g(u)=((arctanu)/(1−u)) +(1/2)u^2 arctanu+(1/2)ln∣1−u∣−(1/4)ln∣1+u^2 ∣−(u/2) +c
$${let}\:{it}\:{be}\:{f}\left({x}\right) \\ $$$${when}\:{stating}\:{u}=\mathrm{1}−\frac{\mathrm{1}}{{x}}\:\Leftrightarrow\:{x}=\frac{\mathrm{1}}{\mathrm{1}−{u}}\:\Rightarrow\:{dx}=\frac{{du}}{\left(\mathrm{1}−{u}\right)^{\mathrm{2}} }\: \\ $$$${f}\left({x}\right)={g}\left({u}\right)=\int\:\left[\frac{\mathrm{1}}{\left(\mathrm{1}−{u}\right)^{\mathrm{2}} }\:+\mathrm{1}\right]{arctanu}\:{du} \\ $$$$\:{by}\:{parts}\:\:\:{A}'=\frac{\mathrm{1}}{\left(\mathrm{1}−{u}\right)^{\mathrm{2}} }\:+{u}\:\:\:\:\:{B}={arctanu}\:\Rightarrow\:{A}=\:\frac{\mathrm{1}}{\mathrm{1}−{u}}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\left({u}^{\mathrm{2}} +\mathrm{1}\right)\:\:\:{and}\:\:{B}'=\:\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }\: \\ $$$${f}\left({x}\right)={g}\left({u}\right)=\:\left[\frac{{arctanu}}{\mathrm{1}−{u}}\:+\frac{\mathrm{1}}{\mathrm{2}}\left({u}^{\mathrm{2}} +\mathrm{1}\right){arctanu}\right]−\int\:\left[\frac{\mathrm{1}}{\left(\mathrm{1}−{u}\right)\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\:+\frac{\mathrm{1}}{\mathrm{2}}\:\right]{du} \\ $$$${Now}\:{let}\:{find}\:\:\:\:{h}\left({u}\right)=\int\:\frac{{du}}{\left(\mathrm{1}−{u}\right)\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\frac{\left({u}^{\mathrm{2}} +\mathrm{1}\right)−\left({u}^{\mathrm{2}} −\mathrm{1}\right)}{\left(\mathrm{1}−{u}\right)\left({u}^{\mathrm{2}} +\mathrm{1}\right)}\:{du}\:\:\: \\ $$$${h}\left({u}\right)=\:\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\left[\frac{\mathrm{1}}{\mathrm{1}−{u}}\:+\:\frac{\mathrm{1}+{u}}{\mathrm{1}+{u}^{\mathrm{2}} }\:\right]\:{du}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{{du}}{\mathrm{1}−{u}}\:\:+\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{4}}\int\:\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }\:{du}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:\frac{−\mathrm{1}}{\mathrm{2}}{ln}\mid\mathrm{1}−{u}\mid\:+\frac{\mathrm{1}}{\mathrm{2}}{arctanu}\:+\frac{\mathrm{1}}{\mathrm{4}}{ln}\mid\mathrm{1}+{u}^{\mathrm{2}} \mid\:+\:{c} \\ $$$${finally}\: \\ $$$$\:{knowing}\:{that}\:{u}=\mathrm{1}−\frac{\mathrm{1}}{{x}}\: \\ $$$${f}\left({x}\right)={g}\left({u}\right)=\frac{{arctanu}}{\mathrm{1}−{u}}\:+\frac{\mathrm{1}}{\mathrm{2}}{u}^{\mathrm{2}} {arctanu}+\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\mathrm{1}−{u}\mid−\frac{\mathrm{1}}{\mathrm{4}}{ln}\mid\mathrm{1}+{u}^{\mathrm{2}} \mid−\frac{{u}}{\mathrm{2}}\:+{c}\: \\ $$$$ \\ $$
Commented by Abdo msup. last updated on 27/Aug/19
thank you sir.
$${thank}\:{you}\:{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *