Menu Close

Find-a-b-c-for-equation-acos-2x-bsin-2-x-c-0-is-satisfied-by-every-x-

Tinku Tara 0 Comments
Pin




Question Number 76622 by Sathvik last updated on 28/Dec/19
Find (a.b.c) for equation acos 2x+bsin^2 x+c=0 is satisfied by every x
$$\mathrm{Find}\:\left(\mathrm{a}.\mathrm{b}.\mathrm{c}\right)\:\mathrm{for}\:\mathrm{equation}\:\mathrm{acos}\:\mathrm{2x}+\mathrm{bsin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{c}=\mathrm{0}\:\mathrm{is}\:\mathrm{satisfied}\:\mathrm{by}\:\mathrm{every}\:\mathrm{x} \\ $$
Answered by MJS last updated on 28/Dec/19
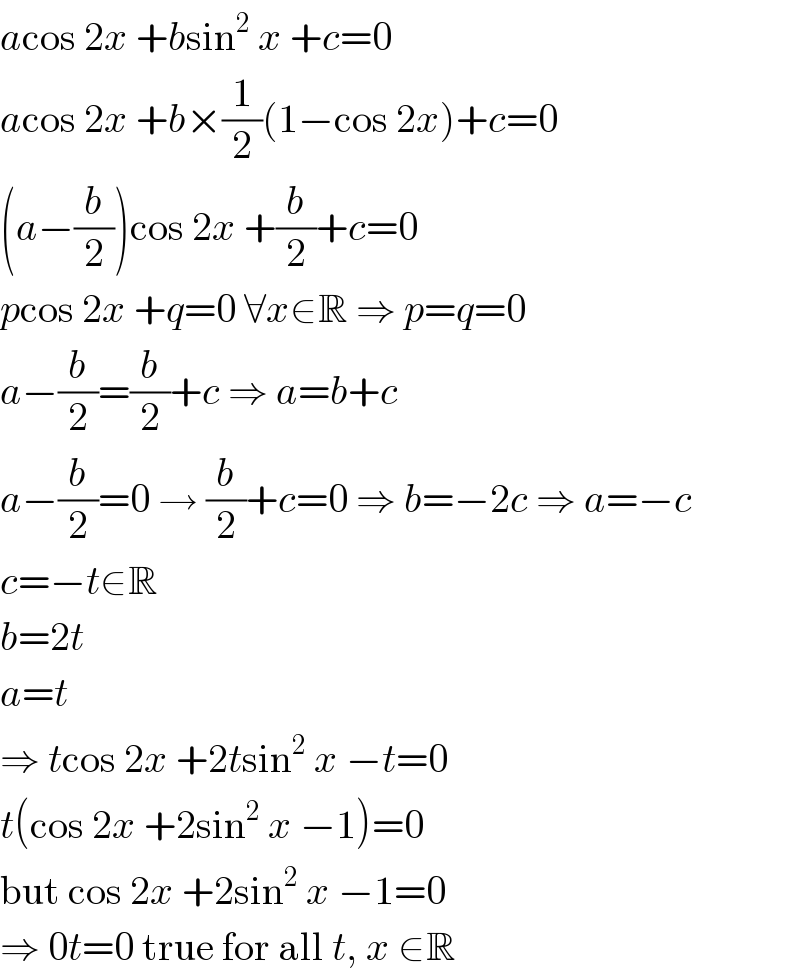
acos 2x +bsin^2 x +c=0 acos 2x +b×(1/2)(1−cos 2x)+c=0 (a−(b/2))cos 2x +(b/2)+c=0 pcos 2x +q=0 ∀x∈R ⇒ p=q=0 a−(b/2)=(b/2)+c ⇒ a=b+c a−(b/2)=0 → (b/2)+c=0 ⇒ b=−2c ⇒ a=−c c=−t∈R b=2t a=t ⇒ tcos 2x +2tsin^2 x −t=0 t(cos 2x +2sin^2 x −1)=0 but cos 2x +2sin^2 x −1=0 ⇒ 0t=0 true for all t, x ∈R
$${a}\mathrm{cos}\:\mathrm{2}{x}\:+{b}\mathrm{sin}^{\mathrm{2}} \:{x}\:+{c}=\mathrm{0} \\ $$$${a}\mathrm{cos}\:\mathrm{2}{x}\:+{b}×\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}{x}\right)+{c}=\mathrm{0} \\ $$$$\left({a}−\frac{{b}}{\mathrm{2}}\right)\mathrm{cos}\:\mathrm{2}{x}\:+\frac{{b}}{\mathrm{2}}+{c}=\mathrm{0} \\ $$$${p}\mathrm{cos}\:\mathrm{2}{x}\:+{q}=\mathrm{0}\:\forall{x}\in\mathbb{R}\:\Rightarrow\:{p}={q}=\mathrm{0} \\ $$$${a}−\frac{{b}}{\mathrm{2}}=\frac{{b}}{\mathrm{2}}+{c}\:\Rightarrow\:{a}={b}+{c} \\ $$$${a}−\frac{{b}}{\mathrm{2}}=\mathrm{0}\:\rightarrow\:\frac{{b}}{\mathrm{2}}+{c}=\mathrm{0}\:\Rightarrow\:{b}=−\mathrm{2}{c}\:\Rightarrow\:{a}=−{c} \\ $$$${c}=−{t}\in\mathbb{R} \\ $$$${b}=\mathrm{2}{t} \\ $$$${a}={t} \\ $$$$\Rightarrow\:{t}\mathrm{cos}\:\mathrm{2}{x}\:+\mathrm{2}{t}\mathrm{sin}^{\mathrm{2}} \:{x}\:−{t}=\mathrm{0} \\ $$$${t}\left(\mathrm{cos}\:\mathrm{2}{x}\:+\mathrm{2sin}^{\mathrm{2}} \:{x}\:−\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{but}\:\mathrm{cos}\:\mathrm{2}{x}\:+\mathrm{2sin}^{\mathrm{2}} \:{x}\:−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{0}{t}=\mathrm{0}\:\mathrm{true}\:\mathrm{for}\:\mathrm{all}\:{t},\:{x}\:\in\mathbb{R} \\ $$
Answered by john santu last updated on 29/Dec/19
acos 2x + b((1/2)−(1/2)cos 2x)=−c (a−(1/2)b)cos 2x=−c−(1/2)b cos 2x=((−2c−b)/(2a−b)) → −1≤((−2c−b)/(2a−b))≤1
$${a}\mathrm{cos}\:\mathrm{2}{x}\:+\:{b}\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2}{x}\right)=−{c} \\ $$$$\left({a}−\frac{\mathrm{1}}{\mathrm{2}}{b}\right)\mathrm{cos}\:\mathrm{2}{x}=−{c}−\frac{\mathrm{1}}{\mathrm{2}}{b} \\ $$$$\mathrm{cos}\:\mathrm{2}{x}=\frac{−\mathrm{2}{c}−{b}}{\mathrm{2}{a}−{b}}\:\rightarrow\:−\mathrm{1}\leqslant\frac{−\mathrm{2}{c}−{b}}{\mathrm{2}{a}−{b}}\leqslant\mathrm{1} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *