Question Number 66544 by naka3546 last updated on 17/Aug/19
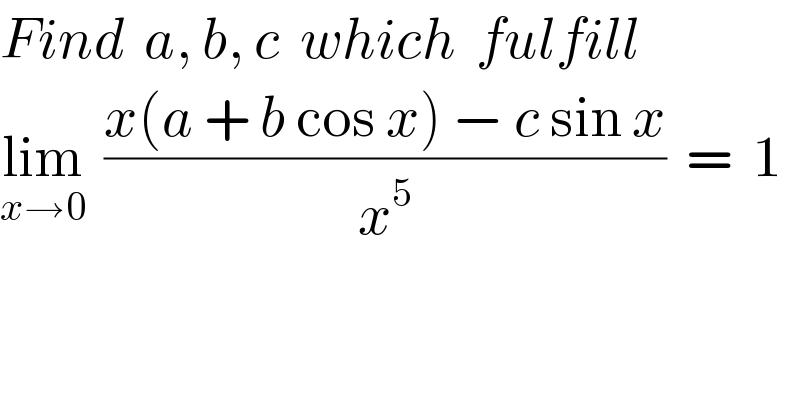
$${Find}\:\:{a},\:{b},\:{c}\:\:{which}\:\:{fulfill}\:\:\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{{x}\left({a}\:+\:{b}\:\mathrm{cos}\:{x}\right)\:−\:{c}\:\mathrm{sin}\:{x}}{{x}^{\mathrm{5}} }\:\:=\:\:\mathrm{1} \\ $$
Answered by Tanmay chaudhury last updated on 17/Aug/19

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{xa}+{bx}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}−\frac{{x}^{\mathrm{6}} }{\mathrm{6}!}\right)−{c}\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+\frac{{x}^{\mathrm{5}} }{\mathrm{5}!}−\frac{{x}^{\mathrm{7}} }{\mathrm{7}!}\right)}{{x}^{\mathrm{5}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{5}} \left(\frac{{b}}{\mathrm{4}!}−\frac{{c}}{\mathrm{5}!}\right)+{x}\left({a}+{b}−{c}\right)+{x}^{\mathrm{3}} \left(\frac{−{b}}{\mathrm{2}!}+\frac{{c}}{\mathrm{3}!}\right)+{othersterms}\:{x}^{\mathrm{5}} }{{x}^{\mathrm{5}} } \\ $$$${when}\:{r}>\mathrm{5} \\ $$$$\:\:\frac{{b}}{\mathrm{24}}−\frac{{c}}{\mathrm{120}}=\mathrm{1} \\ $$$${a}+{b}−{c}=\mathrm{0} \\ $$$$\frac{−{b}}{\mathrm{2}}+\frac{{c}}{\mathrm{6}}=\mathrm{0}\rightarrow{c}=\mathrm{3}{b} \\ $$$$\frac{{b}}{\mathrm{24}}−\frac{\mathrm{3}{b}}{\mathrm{120}}=\mathrm{1} \\ $$$$\frac{\mathrm{5}{b}−\mathrm{3}{b}}{\mathrm{120}}=\mathrm{1}\:\rightarrow\mathrm{2}\boldsymbol{{b}}=\mathrm{120}\:\:\:\boldsymbol{{b}}=\mathrm{60} \\ $$$$\boldsymbol{{c}}=\mathrm{180} \\ $$$$\boldsymbol{{a}}=\boldsymbol{{c}}−\boldsymbol{{b}}\:\:\:\:\:\:\:\:\:\boldsymbol{{a}}=\mathrm{120} \\ $$$$\boldsymbol{{a}}=\mathrm{120}\:\:\:\:\boldsymbol{{b}}=\mathrm{60}\:\:\:\:\boldsymbol{{c}}=\mathrm{180} \\ $$
