Find-a-function-f-x-satisfying-the-following-equation-a-b-1-2-f-x-2-f-x-2-d-dx-f-x-2-dx-0-b-gt-0-a-gt-0-b-a-

Question Number 1581 by 112358 last updated on 21/Aug/15

$${Find}\:{a}\:{function}\:{f}\left({x}\right)\:{satisfying} \\ $$$${the}\:{following}\:{equation}. \\ $$$$\int_{{a}} ^{\:{b}} \left[\frac{\mathrm{1}}{\mathrm{2}}\left\{{f}\left({x}\right)\right\}^{\mathrm{2}} −\sqrt{\left\{{f}\left({x}\right)\right\}^{\mathrm{2}} +\left\{\frac{{d}}{{dx}}\left({f}\left({x}\right)\right)\right\}^{\mathrm{2}} }\right]{dx}=\mathrm{0} \\ $$$${b}>\mathrm{0},{a}>\mathrm{0}\:,\:{b}\neq{a}.\:\: \\ $$

Commented by 123456 last updated on 21/Aug/15

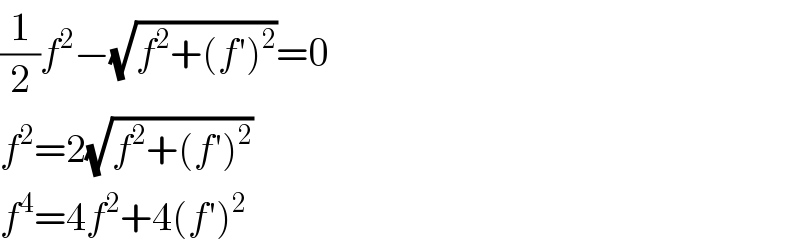
$$\frac{\mathrm{1}}{\mathrm{2}}{f}^{\mathrm{2}} −\sqrt{{f}^{\mathrm{2}} +\left({f}'\right)^{\mathrm{2}} }=\mathrm{0} \\ $$$${f}^{\mathrm{2}} =\mathrm{2}\sqrt{{f}^{\mathrm{2}} +\left({f}'\right)^{\mathrm{2}} } \\ $$$${f}^{\mathrm{4}} =\mathrm{4}{f}^{\mathrm{2}} +\mathrm{4}\left({f}'\right)^{\mathrm{2}} \\ $$

Commented by 112358 last updated on 25/Aug/15

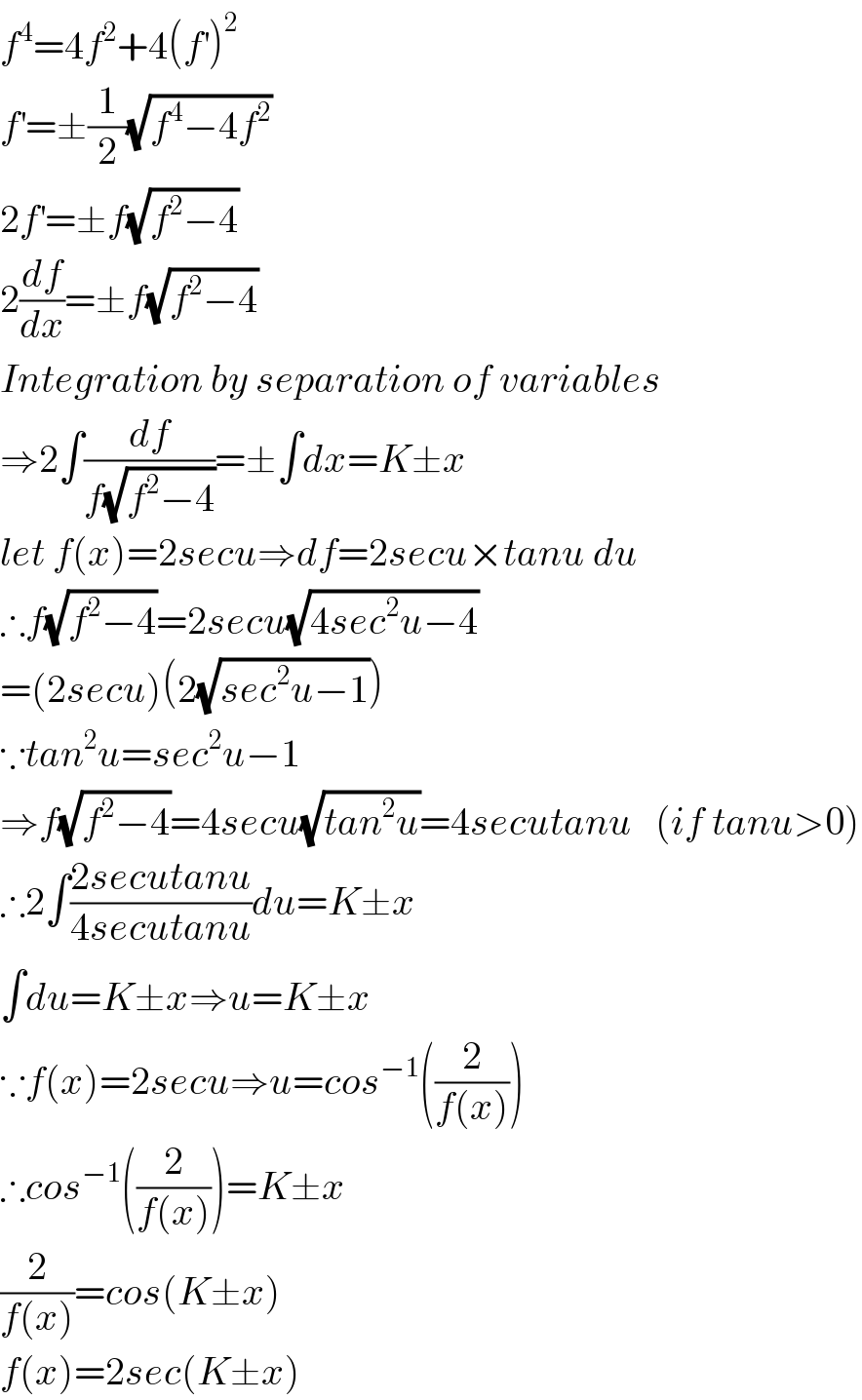
$${f}^{\mathrm{4}} =\mathrm{4}{f}^{\mathrm{2}} +\mathrm{4}\left({f}^{'} \right)^{\mathrm{2}} \\ $$$${f}^{'} =\pm\frac{\mathrm{1}}{\mathrm{2}}\sqrt{{f}^{\mathrm{4}} −\mathrm{4}{f}^{\mathrm{2}} } \\ $$$$\mathrm{2}{f}^{'} =\pm{f}\sqrt{{f}^{\mathrm{2}} −\mathrm{4}} \\ $$$$\mathrm{2}\frac{{df}}{{dx}}=\pm{f}\sqrt{{f}^{\mathrm{2}} −\mathrm{4}} \\ $$$${Integration}\:{by}\:{separation}\:{of}\:{variables} \\ $$$$\Rightarrow\mathrm{2}\int\frac{{df}}{{f}\sqrt{{f}^{\mathrm{2}} −\mathrm{4}}}=\pm\int{dx}={K}\pm{x} \\ $$$${let}\:{f}\left({x}\right)=\mathrm{2}{secu}\Rightarrow{df}=\mathrm{2}{secu}×{tanu}\:{du} \\ $$$$\therefore{f}\sqrt{{f}^{\mathrm{2}} −\mathrm{4}}=\mathrm{2}{secu}\sqrt{\mathrm{4}{sec}^{\mathrm{2}} {u}−\mathrm{4}} \\ $$$$=\left(\mathrm{2}{secu}\right)\left(\mathrm{2}\sqrt{{sec}^{\mathrm{2}} {u}−\mathrm{1}}\right) \\ $$$$\because{tan}^{\mathrm{2}} {u}={sec}^{\mathrm{2}} {u}−\mathrm{1} \\ $$$$\Rightarrow{f}\sqrt{{f}^{\mathrm{2}} −\mathrm{4}}=\mathrm{4}{secu}\sqrt{{tan}^{\mathrm{2}} {u}}=\mathrm{4}{secutanu}\:\:\:\left({if}\:{tanu}>\mathrm{0}\right) \\ $$$$\therefore\mathrm{2}\int\frac{\mathrm{2}{secutanu}}{\mathrm{4}{secutanu}}{du}={K}\pm{x} \\ $$$$\int{du}={K}\pm{x}\Rightarrow{u}={K}\pm{x} \\ $$$$\because{f}\left({x}\right)=\mathrm{2}{secu}\Rightarrow{u}={cos}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{{f}\left({x}\right)}\right) \\ $$$$\therefore{cos}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{{f}\left({x}\right)}\right)={K}\pm{x} \\ $$$$\frac{\mathrm{2}}{{f}\left({x}\right)}={cos}\left({K}\pm{x}\right) \\ $$$${f}\left({x}\right)=\mathrm{2}{sec}\left({K}\pm{x}\right)\:\: \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com