Question Number 76780 by mathmax by abdo last updated on 30/Dec/19
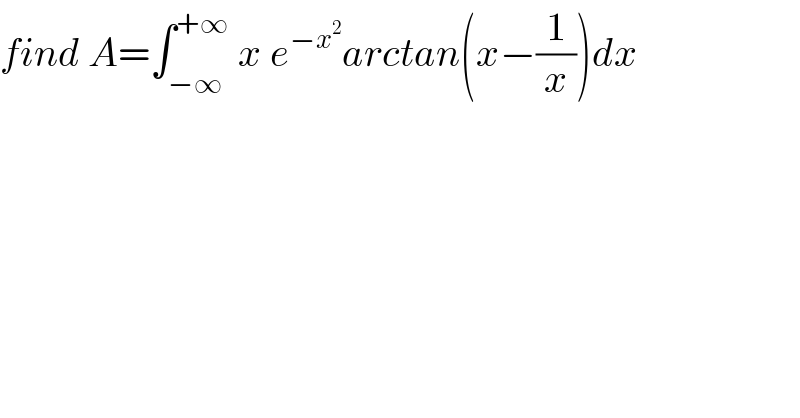
$${find}\:{A}=\int_{−\infty} ^{+\infty} \:{x}\:{e}^{−{x}^{\mathrm{2}} } {arctan}\left({x}−\frac{\mathrm{1}}{{x}}\right){dx} \\ $$
Commented by mathmax by abdo last updated on 06/Jan/20
![by parts u^′ =xe^(−x^2 ) and v=arctan(x−(1/x)) ⇒ A =[−(1/2)e^(−x^2 ) arctan(x−(1/x))]_(−∞) ^(+∞) +(1/2)∫_(−∞) ^(+∞) e^(−x^2 ) ×((1+(1/x^2 ))/(1+(x−(1/x))^2 ))dx =(1/2)∫_(−∞) ^(+∞) (((x^2 +1)e^(−x^2 ) )/(x^2 { 1+(((x^2 −1)^2 )/x^2 )}))dx ⇒2A =∫_(−∞) ^(+∞) (((x^2 +1)e^(−x^2 ) )/(x^2 {((x^2 +(x^2 −1)^2 )/x^2 )}))dx =∫_(−∞) ^(+∞) (((x^2 +1)e^(−x^2 ) )/(x^2 +x^4 −2x^2 +1))dx =∫_(−∞) ^(+∞) (((x^2 +1)e^(−x^2 ) )/(x^4 −x^2 +1))dx let W(z) =(((z^2 +1)e^(−x^2 ) )/(z^4 −z^2 +1)) [poles of W? z^4 −z^2 +1 =0 →t^2 −t+1 =0 (t=z^2 ) Δ=1−4=−3 ⇒t_1 =((1+i(√3))/2) =e^((iπ)/3) and t_2 =((1−i(√3))/2) =e^(−((iπ)/3)) ⇒ W(z) =(((z^2 +1)e^(−z^2 ) )/((z^2 −e^((iπ)/3) )(z^2 −e^(−((iπ)/3)) ))) =(((z^2 +1)e^(−z^2 ) )/((z−e^((iπ)/6) )(z+e^((iπ)/6) )(z−e^(−((iπ)/6)) )(z+e^(−((iπ)/6)) ))) ∫_(−∞) ^(+∞) W(z)dz =2iπ{ Res(W,e^((iπ)/6) ) +Res(W,−e^(−((iπ)/6)) )} ...be continued...](https://www.tinkutara.com/question/Q77502.png)
$${by}\:{parts}\:{u}^{'} ={xe}^{−{x}^{\mathrm{2}} } \:{and}\:{v}={arctan}\left({x}−\frac{\mathrm{1}}{{x}}\right)\:\Rightarrow \\ $$$${A}\:=\left[−\frac{\mathrm{1}}{\mathrm{2}}{e}^{−{x}^{\mathrm{2}} } {arctan}\left({x}−\frac{\mathrm{1}}{{x}}\right)\right]_{−\infty} ^{+\infty} +\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{+\infty} \:{e}^{−{x}^{\mathrm{2}} } ×\frac{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\mathrm{1}+\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} }{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{+\infty} \:\frac{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right){e}^{−{x}^{\mathrm{2}} } }{{x}^{\mathrm{2}} \left\{\:\mathrm{1}+\frac{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right\}}{dx}\:\Rightarrow\mathrm{2}{A}\:=\int_{−\infty} ^{+\infty} \:\frac{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right){e}^{−{x}^{\mathrm{2}} } }{{x}^{\mathrm{2}} \left\{\frac{{x}^{\mathrm{2}} \:+\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right\}}{dx} \\ $$$$=\int_{−\infty} ^{+\infty} \:\frac{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right){e}^{−{x}^{\mathrm{2}} } }{{x}^{\mathrm{2}} +{x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}}{dx}\:=\int_{−\infty} ^{+\infty} \:\frac{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right){e}^{−{x}^{\mathrm{2}} } }{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} \:+\mathrm{1}}{dx} \\ $$$${let}\:{W}\left({z}\right)\:=\frac{\left({z}^{\mathrm{2}} \:+\mathrm{1}\right){e}^{−{x}^{\mathrm{2}} } }{{z}^{\mathrm{4}} −{z}^{\mathrm{2}} \:+\mathrm{1}}\:\left[{poles}\:{of}\:{W}?\right. \\ $$$${z}^{\mathrm{4}} −{z}^{\mathrm{2}} \:+\mathrm{1}\:=\mathrm{0}\:\rightarrow{t}^{\mathrm{2}} −{t}+\mathrm{1}\:=\mathrm{0}\:\:\left({t}={z}^{\mathrm{2}} \right) \\ $$$$\Delta=\mathrm{1}−\mathrm{4}=−\mathrm{3}\:\Rightarrow{t}_{\mathrm{1}} =\frac{\mathrm{1}+{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:={e}^{\frac{{i}\pi}{\mathrm{3}}} \:{and}\:{t}_{\mathrm{2}} =\frac{\mathrm{1}−{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:={e}^{−\frac{{i}\pi}{\mathrm{3}}} \:\Rightarrow \\ $$$${W}\left({z}\right)\:=\frac{\left({z}^{\mathrm{2}} \:+\mathrm{1}\right){e}^{−{z}^{\mathrm{2}} } }{\left({z}^{\mathrm{2}} −{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\left({z}^{\mathrm{2}} −{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)}\:=\frac{\left({z}^{\mathrm{2}} \:+\mathrm{1}\right){e}^{−{z}^{\mathrm{2}} } }{\left({z}−{e}^{\frac{{i}\pi}{\mathrm{6}}} \right)\left({z}+{e}^{\frac{{i}\pi}{\mathrm{6}}} \right)\left({z}−{e}^{−\frac{{i}\pi}{\mathrm{6}}} \right)\left({z}+{e}^{−\frac{{i}\pi}{\mathrm{6}}} \right)} \\ $$$$\int_{−\infty} ^{+\infty} \:{W}\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:{Res}\left({W},{e}^{\frac{{i}\pi}{\mathrm{6}}} \right)\:+{Res}\left({W},−{e}^{−\frac{{i}\pi}{\mathrm{6}}} \right)\right\} \\ $$$$…{be}\:{continued}… \\ $$$$ \\ $$$$ \\ $$
