Question Number 9727 by geovane10math last updated on 29/Dec/16
![Find a x integer: [Σ_(k=1) ^∞ ((sin(2Πkxπ))/k)] + [Σ_(k=1) ^∞ ((sin(2Πkxe))/k)] = 0 Where: 𝚷 represents 180° ; 𝛑 represents 3,14159265358... .](https://www.tinkutara.com/question/Q9727.png)
$$\mathrm{Find}\:\mathrm{a}\:\boldsymbol{{x}}\:{integer}: \\ $$$$\left[\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}\left(\mathrm{2}\Pi{kx}\pi\right)}{{k}}\right]\:+\:\left[\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}\left(\mathrm{2}\Pi{kxe}\right)}{{k}}\right]\:=\:\mathrm{0}\: \\ $$$$ \\ $$$$\boldsymbol{\mathrm{Where}}: \\ $$$$\boldsymbol{\Pi}\:\mathrm{represents}\:\mathrm{180}°\:; \\ $$$$\boldsymbol{\pi}\:\mathrm{represents}\:\mathrm{3},\mathrm{14159265358}…\:. \\ $$
Commented by prakash jain last updated on 29/Dec/16
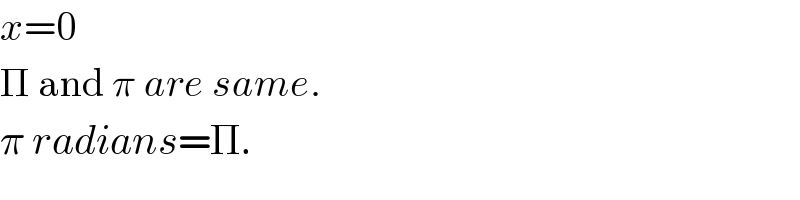
$${x}=\mathrm{0} \\ $$$$\Pi\:\mathrm{and}\:\pi\:{are}\:{same}. \\ $$$$\pi\:{radians}=\Pi. \\ $$
Commented by geovane10math last updated on 29/Dec/16

$${ok}\:{thanks},\:{but}\:{there}\:{is}\:{a}\:{solution}\:\neq\:\mathrm{0}???? \\ $$$$ \\ $$
Commented by FilupSmith last updated on 29/Dec/16
![[Σ_(k=1) ^∞ ((sin(2Πkxπ))/k)] + [Σ_(k=1) ^∞ ((sin(2Πkxe))/k)] = 0 Π=π ∴Σ_(k=1) ^∞ ((sin(2π^2 kx)+sin(2πekx))/k)=0 one situation: sin(2π^2 kx)+sin(2πekx)=0 working](https://www.tinkutara.com/question/Q9737.png)
$$\left[\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}\left(\mathrm{2}\Pi{kx}\pi\right)}{{k}}\right]\:+\:\left[\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}\left(\mathrm{2}\Pi{kxe}\right)}{{k}}\right]\:=\:\mathrm{0} \\ $$$$\Pi=\pi \\ $$$$\therefore\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}\left(\mathrm{2}\pi^{\mathrm{2}} {kx}\right)+\mathrm{sin}\left(\mathrm{2}\pi{ekx}\right)}{{k}}=\mathrm{0} \\ $$$$\: \\ $$$$\boldsymbol{\mathrm{one}}\:\boldsymbol{\mathrm{situation}}: \\ $$$$\mathrm{sin}\left(\mathrm{2}\pi^{\mathrm{2}} {kx}\right)+\mathrm{sin}\left(\mathrm{2}\pi{ekx}\right)=\mathrm{0} \\ $$$$ \\ $$$${working} \\ $$
Commented by geovane10math last updated on 29/Dec/16

$${Friend},\:{if}\:{you}\:{find}\:{a}\:{integer}\:{and}\:{non}-{zero} \\ $$$${solution},\:{congratulations}!,\:{you}\:{proved} \\ $$$${that}\:\boldsymbol{\pi}\:+\:\boldsymbol{{e}}\:{is}\:{rational}\:\left({this}\:{is}\:{a}\:{open}\:{problem}\right) \\ $$$$ \\ $$$${If}\:{don}'{t}\:{exists}\:{x}\:{integer},\:{so}\:\boldsymbol{\pi}\:+\:\boldsymbol{{e}}\:{is} \\ $$$${irrational} \\ $$$$ \\ $$$${I}\:{can}\:{show}\:{you}\:{why}\:{find}\:{this}\:\boldsymbol{{x}}\:{solve} \\ $$$${this}\:{problem} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$\boldsymbol{\mathrm{OK}}\:\:???????????? \\ $$
Commented by geovane10math last updated on 29/Dec/16
![THE PROOF THAT 𝛑 + e IS IRRATIONAL Consider {π + e = (y/x) ∣ x,y ∈ Z, x ≠ 0} xπ + xe = y y is a integer: xπ + xe = y,0 We know that 0,999...=1 , so, if we sum both the sides by (y−1) we have: (y−1),999... = y=y,0 xπ + xe = (y−1),999... Proposition: If q is rational and k is irra- tional, so qk is irrational. Demonstration: Suppose that this product is rational. qk = Q k = (Q/q) An irrational cannot be a ratio between rationals. ■ So, x𝛑 and xe are both irrationals. If they′re irrationals, so the decimal part is a infinite number that don′t repeat (if repeat, is a periodic tithe). xπ + xe = (y−1),999... For this equation to be true, the sum of the decimal part of x𝛑 and the decimal part of xe must be 0,999... (if results in something different, you can see that the equation would be wrong). The decimal part (or fractional part) is the number of decimal places. Frac(s) = s − ⌊s⌋ ⌊s⌋ = floor function Notation: Frac(s) = {s} So, {xπ} + {xe} = 0,999... {xπ} + {xe} = 1 In Wikipedia, search in Floor and Ceiling functions, you find the formula ⌊s⌋ = s − (1/2) + (1/π)Σ_(k=1) ^∞ ((sin(2πks))/k) So, {s} = (1/2) − (1/π)Σ_(k=1) ^∞ ((sin(2πks))/k) {xπ} + {xe} = 1 (1/2) − (1/π)Σ_(k=1) ^∞ ((sin(2πk∙xπ))/k) + (1/2) − (1/π)Σ_(k=1) ^∞ ((sin(2πk∙xe))/k)=1 1 − (1/π)[Σ_(k=1) ^∞ ((sin(2πk∙xπ))/k) + Σ_(k=1) ^∞ ((sin(2πk∙xe))/k)]=1 − (1/π)[Σ_(k=1) ^∞ ((sin(2πk∙xπ))/k) + Σ_(k=1) ^∞ ((sin(2πk∙xe))/k)]=0 Σ_(k=1) ^∞ ((sin(2πk∙xπ))/k) + Σ_(k=1) ^∞ ((sin(2πk∙xe))/k) = 0 Good luck! ;) Caution: π and Π are not equals (I think) because π = 3,141... Π = 180° = π rad π = π rad → it′s wrong](https://www.tinkutara.com/question/Q9740.png)
$$\mathrm{THE}\:\mathrm{PROOF}\:\mathrm{THAT}\:\boldsymbol{\pi}\:+\:\boldsymbol{{e}}\:\mathrm{IS}\:\mathrm{IRRATIONAL} \\ $$$${Consider}\:\left\{\pi\:+\:{e}\:=\:\frac{{y}}{{x}}\:\mid\:{x},{y}\:\in\:\mathbb{Z},\:{x}\:\neq\:\mathrm{0}\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}\pi\:+\:{xe}\:=\:{y} \\ $$$$\:{y}\:{is}\:{a}\:{integer}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}\pi\:+\:{xe}\:=\:{y},\mathrm{0} \\ $$$$\:{We}\:{know}\:{that}\:\:\mathrm{0},\mathrm{999}…=\mathrm{1}\:,\:{so},\:{if}\:{we}\:{sum} \\ $$$${both}\:{the}\:{sides}\:{by}\:\left({y}−\mathrm{1}\right)\:{we}\:{have}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({y}−\mathrm{1}\right),\mathrm{999}…\:=\:{y}={y},\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}\pi\:+\:{xe}\:=\:\left({y}−\mathrm{1}\right),\mathrm{999}… \\ $$$$\mathrm{Proposition}:\:\mathrm{If}\:\boldsymbol{\mathrm{q}}\:\mathrm{is}\:\mathrm{rational}\:\mathrm{and}\:\boldsymbol{\mathrm{k}}\:\mathrm{is}\:\mathrm{irra}- \\ $$$$\mathrm{tional},\:\mathrm{so}\:\boldsymbol{\mathrm{qk}}\:\mathrm{is}\:\mathrm{irrational}. \\ $$$$\mathrm{Demonstration}:\:\mathrm{Suppose}\:\mathrm{that}\:\mathrm{this}\:\mathrm{product} \\ $$$$\mathrm{is}\:\mathrm{rational}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{qk}}\:=\:\boldsymbol{\mathrm{Q}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{k}}\:=\:\frac{\boldsymbol{\mathrm{Q}}}{\boldsymbol{\mathrm{q}}} \\ $$$$\mathrm{An}\:\mathrm{irrational}\:\mathrm{cannot}\:\mathrm{be}\:\mathrm{a}\:\mathrm{ratio}\:\mathrm{between} \\ $$$$\mathrm{rationals}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\blacksquare \\ $$$$\:\mathrm{So},\:\boldsymbol{{x}\pi}\:\mathrm{and}\:\boldsymbol{{xe}}\:\mathrm{are}\:\mathrm{both}\:\mathrm{irrationals}.\:\mathrm{If} \\ $$$$\mathrm{they}'\mathrm{re}\:\mathrm{irrationals},\:\mathrm{so}\:\mathrm{the}\:\mathrm{decimal}\:\mathrm{part}\:\mathrm{is} \\ $$$$\mathrm{a}\:\mathrm{infinite}\:\mathrm{number}\:\mathrm{that}\:\mathrm{don}'\mathrm{t}\:\mathrm{repeat}\:\left(\mathrm{if}\:\mathrm{repeat},\right. \\ $$$$\left.\mathrm{is}\:\mathrm{a}\:\mathrm{periodic}\:\mathrm{tithe}\right). \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}\pi\:+\:{xe}\:=\:\left({y}−\mathrm{1}\right),\mathrm{999}… \\ $$$$\mathrm{For}\:\mathrm{this}\:\mathrm{equation}\:\mathrm{to}\:\mathrm{be}\:\mathrm{true},\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{decimal}\:\mathrm{part}\:\mathrm{of}\:\boldsymbol{{x}\pi}\:\mathrm{and}\:\mathrm{the}\:\mathrm{decimal} \\ $$$$\mathrm{part}\:\mathrm{of}\:\boldsymbol{{xe}}\:\mathrm{must}\:\mathrm{be}\:\mathrm{0},\mathrm{999}…\:\left(\mathrm{if}\:\mathrm{results}\:\mathrm{in}\right. \\ $$$$\mathrm{something}\:\mathrm{different},\:\mathrm{you}\:\mathrm{can}\:\mathrm{see}\:\mathrm{that} \\ $$$$\left.\mathrm{the}\:\mathrm{equation}\:\mathrm{would}\:\mathrm{be}\:\mathrm{wrong}\right). \\ $$$$ \\ $$$$\mathrm{The}\:\mathrm{decimal}\:\mathrm{part}\:\left(\mathrm{or}\:\mathrm{fractional}\:\mathrm{part}\right)\:\mathrm{is} \\ $$$$\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{decimal}\:\mathrm{places}.\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{Frac}\left({s}\right)\:=\:{s}\:−\:\lfloor{s}\rfloor \\ $$$$\lfloor{s}\rfloor\:=\:{floor}\:{function} \\ $$$${Notation}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{Frac}\left({s}\right)\:=\:\left\{{s}\right\} \\ $$$$\mathrm{So}, \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left\{{x}\pi\right\}\:+\:\left\{{xe}\right\}\:=\:\mathrm{0},\mathrm{999}… \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left\{{x}\pi\right\}\:+\:\left\{{xe}\right\}\:=\:\mathrm{1} \\ $$$$\mathrm{In}\:\mathrm{Wikipedia},\:\mathrm{search}\:\mathrm{in}\:\mathrm{Floor}\:\mathrm{and}\:\mathrm{Ceiling} \\ $$$$\mathrm{functions},\:\mathrm{you}\:\mathrm{find}\:\mathrm{the}\:\mathrm{formula} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\lfloor{s}\rfloor\:=\:{s}\:−\:\frac{\mathrm{1}}{\mathrm{2}}\:+\:\frac{\mathrm{1}}{\pi}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}\left(\mathrm{2}\pi{ks}\right)}{{k}} \\ $$$$\mathrm{So}, \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left\{{s}\right\}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:−\:\frac{\mathrm{1}}{\pi}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}\left(\mathrm{2}\pi{ks}\right)}{{k}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left\{{x}\pi\right\}\:+\:\left\{{xe}\right\}\:=\:\mathrm{1} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\:−\:\frac{\mathrm{1}}{\pi}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}\left(\mathrm{2}\pi{k}\centerdot{x}\pi\right)}{{k}}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\:−\:\frac{\mathrm{1}}{\pi}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}\left(\mathrm{2}\pi{k}\centerdot{xe}\right)}{{k}}=\mathrm{1} \\ $$$$\mathrm{1}\:−\:\frac{\mathrm{1}}{\pi}\left[\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}\left(\mathrm{2}\pi{k}\centerdot{x}\pi\right)}{{k}}\:+\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}\left(\mathrm{2}\pi{k}\centerdot{xe}\right)}{{k}}\right]=\mathrm{1} \\ $$$$−\:\frac{\mathrm{1}}{\pi}\left[\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}\left(\mathrm{2}\pi{k}\centerdot{x}\pi\right)}{{k}}\:+\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}\left(\mathrm{2}\pi{k}\centerdot{xe}\right)}{{k}}\right]=\mathrm{0} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}\left(\mathrm{2}\pi{k}\centerdot{x}\pi\right)}{{k}}\:+\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}\left(\mathrm{2}\pi{k}\centerdot{xe}\right)}{{k}}\:=\:\mathrm{0} \\ $$$$\left.\mathrm{Good}\:\mathrm{luck}!\:\:;\right) \\ $$$${Caution}:\:\pi\:{and}\:\Pi\:{are}\:{not}\:{equals}\:\left({I}\:{think}\right) \\ $$$${because} \\ $$$$\pi\:=\:\mathrm{3},\mathrm{141}…\:\:\:\:\:\:\:\:\:\Pi\:=\:\mathrm{180}°\:=\:\pi\:\mathrm{rad} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\pi\:=\:\pi\:\mathrm{rad}\:\rightarrow\:{it}'{s}\:{wrong} \\ $$$$ \\ $$
Commented by prakash jain last updated on 30/Dec/16

$$\mathrm{when}\:\mathrm{we}\:\mathrm{write}\:\mathrm{sin}{x}\:\mathrm{usualy}\:\mathrm{notation} \\ $$$$\mathrm{is}\:{x}\:\mathrm{is}\:\mathrm{in}\:\mathrm{radians}. \\ $$$$\mathrm{sin}\:\pi=\mathrm{sin}\:\mathrm{180}° \\ $$$$\Pi\:\mathrm{is}\:\mathrm{given}\:\mathrm{as}\:\mathrm{equivalent}\:\mathrm{to}\:\mathrm{180}°\:\mathrm{so} \\ $$$$\Pi=\pi\:\mathrm{radians} \\ $$$$\mathrm{sin}\:\Pi=\mathrm{sin}\:\pi \\ $$$$ \\ $$$$\mathrm{sin}\:\mathrm{2}\pi=\mathrm{0}\:\mathrm{since}\:\pi=\mathrm{3}.\mathrm{14}..\:\equiv\mathrm{180}° \\ $$$$\mathrm{sin}\:\mathrm{2}\Pi=\mathrm{0}\:\mathrm{in}\:\mathrm{the}\:\mathrm{given}\:\mathrm{question}. \\ $$$$ \\ $$
