Question Number 680 by 123456 last updated on 23/Feb/15
![find all f:N→N such that f[n+f(n)]=2f(n)](https://www.tinkutara.com/question/Q680.png)
$${find}\:{all}\:{f}:\mathbb{N}\rightarrow\mathbb{N}\:{such}\:{that} \\ $$$${f}\left[{n}+{f}\left({n}\right)\right]=\mathrm{2}{f}\left({n}\right) \\ $$
Answered by prakash jain last updated on 23/Feb/15
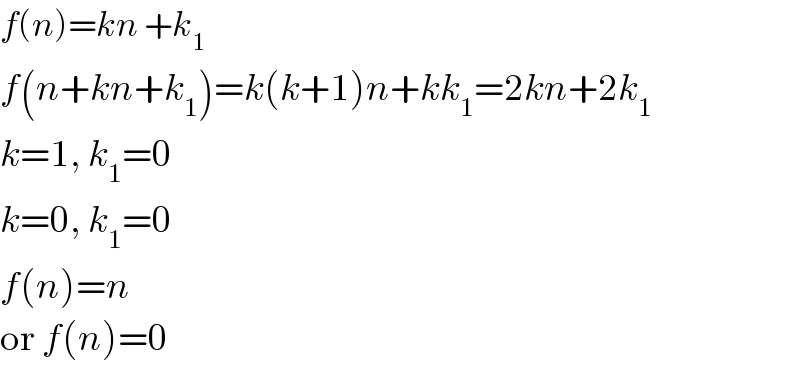
$${f}\left({n}\right)={kn}\:+{k}_{\mathrm{1}} \\ $$$${f}\left({n}+{kn}+{k}_{\mathrm{1}} \right)={k}\left({k}+\mathrm{1}\right){n}+{kk}_{\mathrm{1}} =\mathrm{2}{kn}+\mathrm{2}{k}_{\mathrm{1}} \\ $$$${k}=\mathrm{1},\:{k}_{\mathrm{1}} =\mathrm{0} \\ $$$${k}=\mathrm{0},\:{k}_{\mathrm{1}} =\mathrm{0} \\ $$$${f}\left({n}\right)={n} \\ $$$$\mathrm{or}\:{f}\left({n}\right)=\mathrm{0} \\ $$
