Question Number 142570 by mathsuji last updated on 02/Jun/21

$${Find}\:{all}\:{functions}\:{f}:\mathbb{R}\rightarrow\mathbb{R}\:{such}\:{that} \\ $$$${f}\left({x}+{y}\right)=\mathrm{2}{f}\left({x}\right)+\mathrm{3}{f}\left({y}\right)−\mathrm{4}{xyf}\left(\mathrm{2}{x}−\mathrm{3}{y}\right) \\ $$$$\left(\forall{x};{y}\in\mathbb{R}\right) \\ $$
Answered by ajfour last updated on 02/Jun/21
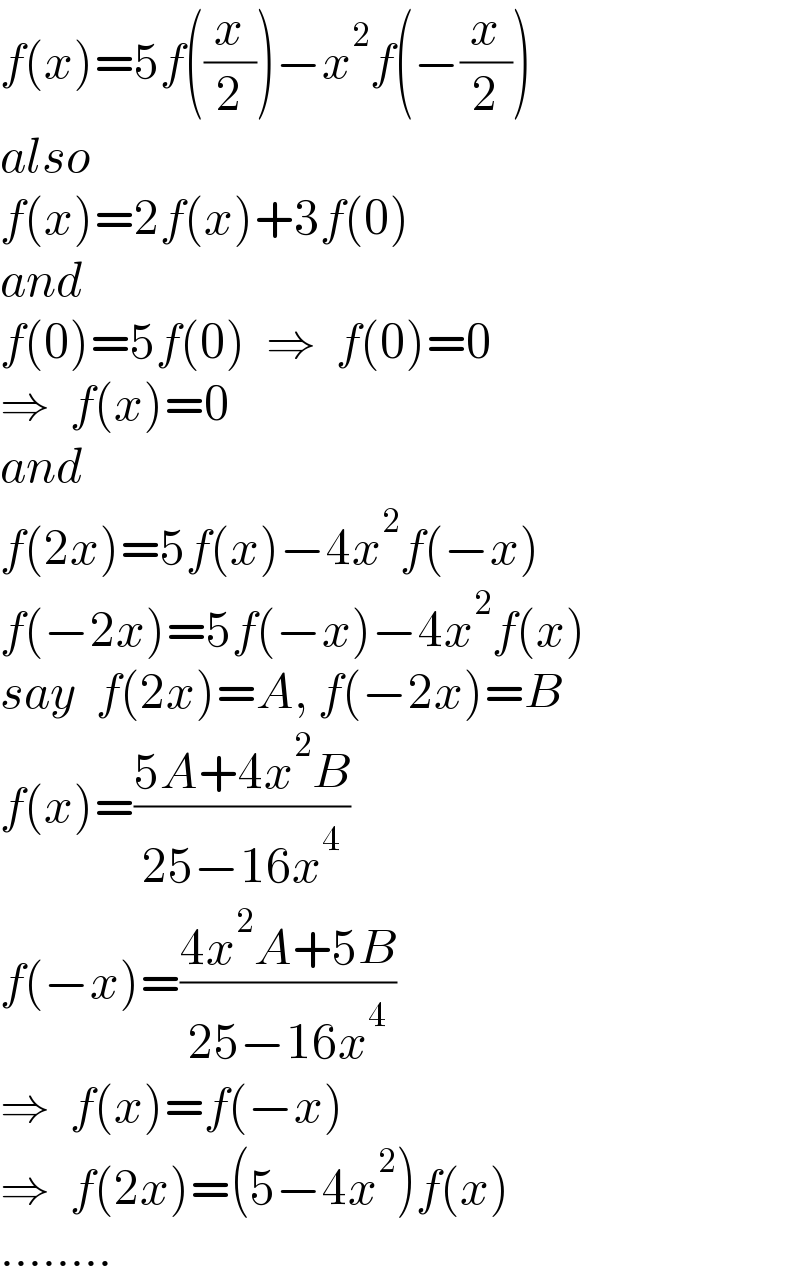
$${f}\left({x}\right)=\mathrm{5}{f}\left(\frac{{x}}{\mathrm{2}}\right)−{x}^{\mathrm{2}} {f}\left(−\frac{{x}}{\mathrm{2}}\right) \\ $$$${also} \\ $$$${f}\left({x}\right)=\mathrm{2}{f}\left({x}\right)+\mathrm{3}{f}\left(\mathrm{0}\right) \\ $$$${and} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{5}{f}\left(\mathrm{0}\right)\:\:\Rightarrow\:\:{f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\:{f}\left({x}\right)=\mathrm{0} \\ $$$${and} \\ $$$${f}\left(\mathrm{2}{x}\right)=\mathrm{5}{f}\left({x}\right)−\mathrm{4}{x}^{\mathrm{2}} {f}\left(−{x}\right) \\ $$$${f}\left(−\mathrm{2}{x}\right)=\mathrm{5}{f}\left(−{x}\right)−\mathrm{4}{x}^{\mathrm{2}} {f}\left({x}\right) \\ $$$${say}\:\:{f}\left(\mathrm{2}{x}\right)={A},\:{f}\left(−\mathrm{2}{x}\right)={B} \\ $$$${f}\left({x}\right)=\frac{\mathrm{5}{A}+\mathrm{4}{x}^{\mathrm{2}} {B}}{\mathrm{25}−\mathrm{16}{x}^{\mathrm{4}} } \\ $$$${f}\left(−{x}\right)=\frac{\mathrm{4}{x}^{\mathrm{2}} {A}+\mathrm{5}{B}}{\mathrm{25}−\mathrm{16}{x}^{\mathrm{4}} } \\ $$$$\Rightarrow\:\:{f}\left({x}\right)={f}\left(−{x}\right) \\ $$$$\Rightarrow\:\:{f}\left(\mathrm{2}{x}\right)=\left(\mathrm{5}−\mathrm{4}{x}^{\mathrm{2}} \right){f}\left({x}\right) \\ $$$$…….. \\ $$
