Question Number 6133 by sanusihammed last updated on 15/Jun/16
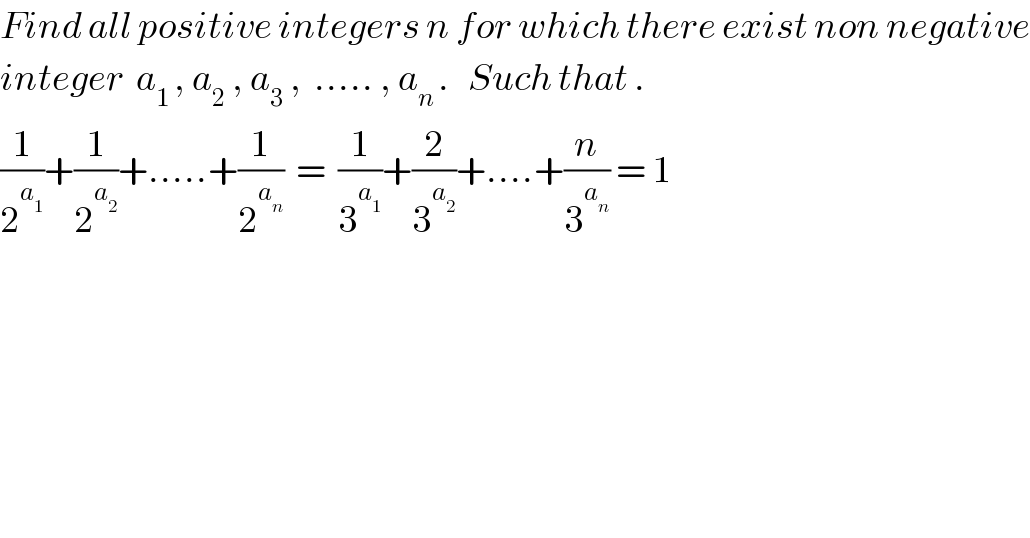
$${Find}\:{all}\:{positive}\:{integers}\:{n}\:{for}\:{which}\:{there}\:{exist}\:{non}\:{negative} \\ $$$${integer}\:\:{a}_{\mathrm{1}\:} ,\:{a}_{\mathrm{2}} \:,\:{a}_{\mathrm{3}} \:,\:\:…..\:,\:{a}_{{n}\:} .\:\:\:{Such}\:{that}\:. \\ $$$$\frac{\mathrm{1}}{\mathrm{2}^{{a}_{\mathrm{1}} } }+\frac{\mathrm{1}}{\mathrm{2}^{{a}_{\mathrm{2}} } }+…..+\frac{\mathrm{1}}{\mathrm{2}^{{a}_{{n}} } }\:\:=\:\:\frac{\mathrm{1}}{\mathrm{3}^{{a}_{\mathrm{1}} } }+\frac{\mathrm{2}}{\mathrm{3}^{{a}_{\mathrm{2}} } }+….+\frac{{n}}{\mathrm{3}^{{a}_{{n}} } }\:=\:\mathrm{1} \\ $$
Commented by prakash jain last updated on 15/Jun/16
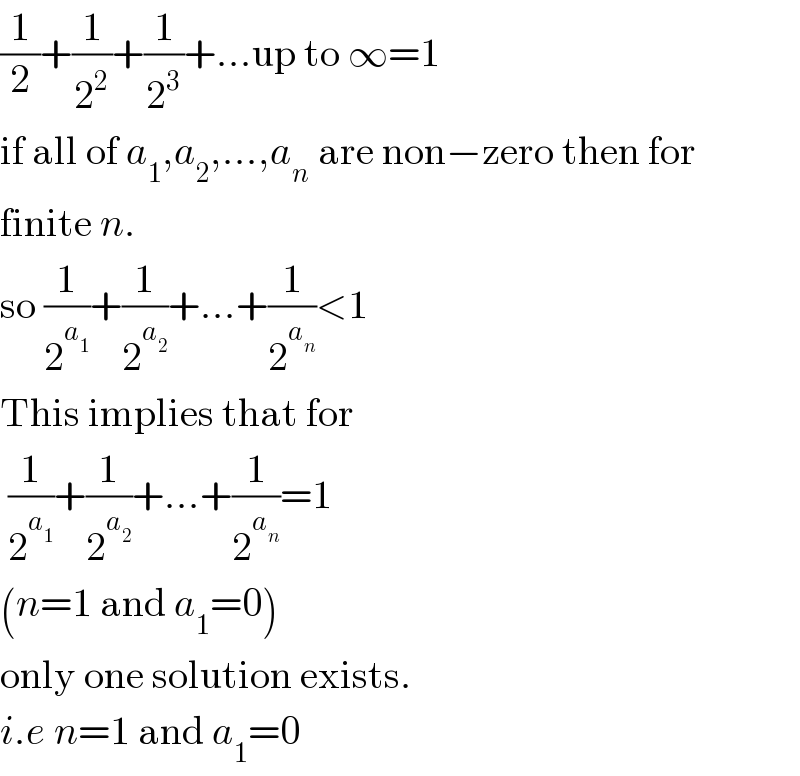
$$\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }+…\mathrm{up}\:\mathrm{to}\:\infty=\mathrm{1} \\ $$$$\mathrm{if}\:\mathrm{all}\:\mathrm{of}\:{a}_{\mathrm{1}} ,{a}_{\mathrm{2}} ,…,{a}_{{n}} \:\mathrm{are}\:\mathrm{non}−\mathrm{zero}\:\mathrm{then}\:\mathrm{for} \\ $$$$\mathrm{finite}\:{n}. \\ $$$$\mathrm{so}\:\frac{\mathrm{1}}{\mathrm{2}^{{a}_{\mathrm{1}} } }+\frac{\mathrm{1}}{\mathrm{2}^{{a}_{\mathrm{2}} } }+…+\frac{\mathrm{1}}{\mathrm{2}^{{a}_{{n}} } }<\mathrm{1}\: \\ $$$$\mathrm{This}\:\mathrm{implies}\:\mathrm{that}\:\mathrm{for} \\ $$$$\:\frac{\mathrm{1}}{\mathrm{2}^{{a}_{\mathrm{1}} } }+\frac{\mathrm{1}}{\mathrm{2}^{{a}_{\mathrm{2}} } }+…+\frac{\mathrm{1}}{\mathrm{2}^{{a}_{{n}} } }=\mathrm{1}\: \\ $$$$\left({n}=\mathrm{1}\:\mathrm{and}\:{a}_{\mathrm{1}} =\mathrm{0}\right) \\ $$$$\mathrm{only}\:\mathrm{one}\:\mathrm{solution}\:\mathrm{exists}. \\ $$$${i}.{e}\:{n}=\mathrm{1}\:\mathrm{and}\:{a}_{\mathrm{1}} =\mathrm{0} \\ $$
