Question Number 1379 by 314159 last updated on 27/Jul/15

$${Find}\:{all}\:{positive}\:{integers}\:{n}\:{such}\:{that}\:\: \\ $$$${n}\leqslant\mathrm{2014}\:{and}\:\mathrm{3}^{{n}−\mathrm{1}} .{n}\:\:{will}\:{be}\:{a}\:{perfect}\:{square}\:{integer}. \\ $$
Commented by 123456 last updated on 26/Jul/15

$${m}\equiv\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}\left(\mathrm{mod}\:\mathrm{5}\right) \\ $$$${n}={m}^{\mathrm{2}} \equiv\mathrm{0},\mathrm{1},\mathrm{4}\left(\mathrm{mod}\:\mathrm{5}\right) \\ $$$${n}−\mathrm{1}\equiv\mathrm{0}\left(\mathrm{mod}\:\mathrm{2}\right) \\ $$$${n}\equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{2}\right) \\ $$$$\mathrm{N}.\mathrm{C}:\begin{cases}{{n}\equiv\mathrm{0}\left(\mathrm{mod}\:\mathrm{5}\right)\vee{n}\equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{5}\right)\vee{n}\equiv\mathrm{4}\left(\mathrm{mod5}\right)}\\{{n}\equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{2}\right)}\end{cases} \\ $$
Commented by 314159 last updated on 27/Jul/15
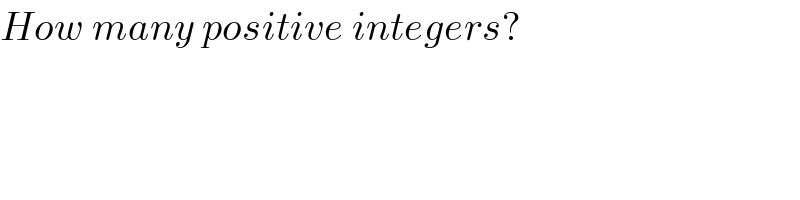
$${How}\:{many}\:{positive}\:{integers}? \\ $$
Commented by prakash jain last updated on 27/Jul/15
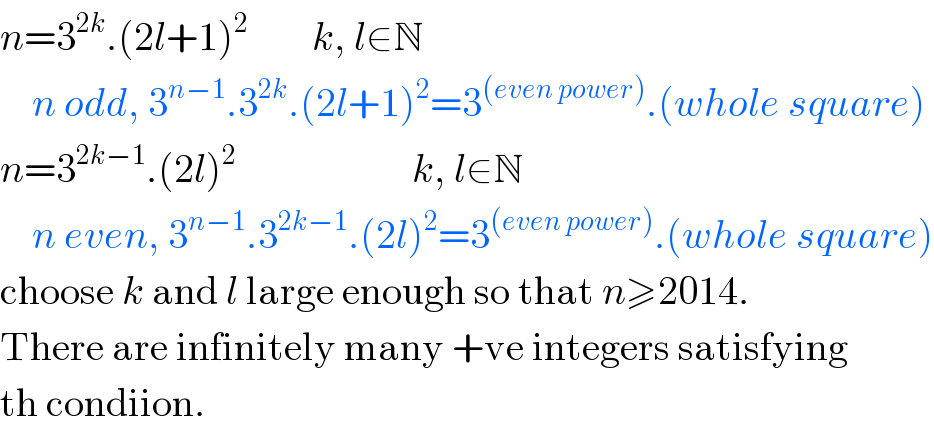
$${n}=\mathrm{3}^{\mathrm{2}{k}} .\left(\mathrm{2}{l}+\mathrm{1}\right)^{\mathrm{2}} \:\:\:\:\:\:\:\:{k},\:{l}\in\mathbb{N} \\ $$$$\:\:\:\:{n}\:{odd},\:\mathrm{3}^{{n}−\mathrm{1}} .\mathrm{3}^{\mathrm{2}{k}} .\left(\mathrm{2}{l}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{3}^{\left({even}\:{power}\right)} .\left({whole}\:{square}\right) \\ $$$${n}=\mathrm{3}^{\mathrm{2}{k}−\mathrm{1}} .\left(\mathrm{2}{l}\right)^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{k},\:{l}\in\mathbb{N} \\ $$$$\:\:\:\:{n}\:{even},\:\mathrm{3}^{{n}−\mathrm{1}} .\mathrm{3}^{\mathrm{2}{k}−\mathrm{1}} .\left(\mathrm{2}{l}\right)^{\mathrm{2}} =\mathrm{3}^{\left({even}\:{power}\right)} .\left({whole}\:{square}\right) \\ $$$$\mathrm{choose}\:{k}\:\mathrm{and}\:{l}\:\mathrm{large}\:\mathrm{enough}\:\mathrm{so}\:\mathrm{that}\:{n}\geqslant\mathrm{2014}. \\ $$$$\mathrm{There}\:\mathrm{are}\:\mathrm{infinitely}\:\mathrm{many}\:+\mathrm{ve}\:\mathrm{integers}\:\mathrm{satisfying} \\ $$$$\mathrm{th}\:\mathrm{condiion}. \\ $$
Commented by 314159 last updated on 27/Jul/15
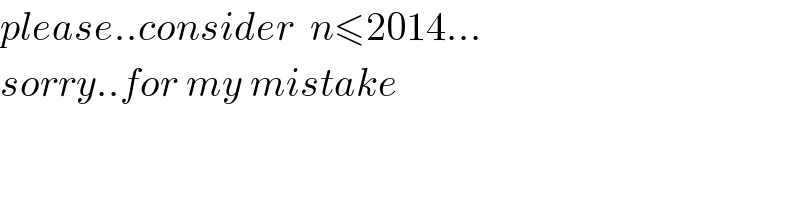
$${please}..{consider}\:\:{n}\leqslant\mathrm{2014}… \\ $$$${sorry}..{for}\:{my}\:{mistake} \\ $$
Commented by 314159 last updated on 28/Jul/15
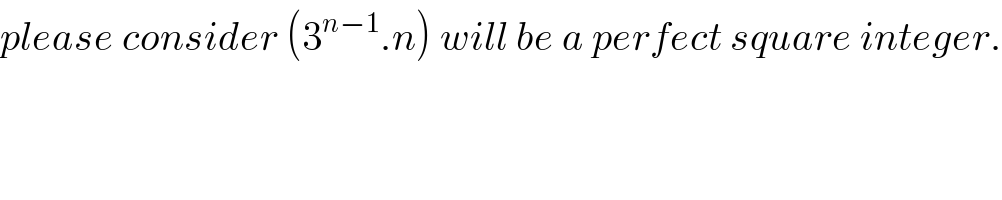
$${please}\:{consider}\:\left(\mathrm{3}^{{n}−\mathrm{1}} .{n}\right)\:{will}\:{be}\:{a}\:{perfect}\:{square}\:{integer}. \\ $$
