Question Number 131713 by mohammad17 last updated on 07/Feb/21
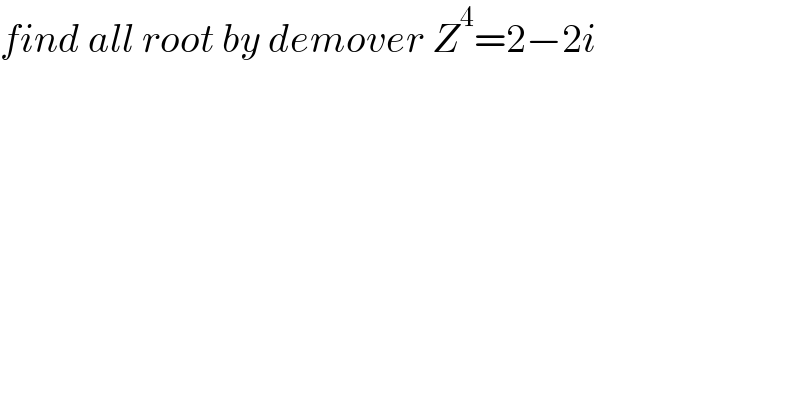
$${find}\:{all}\:{root}\:{by}\:{demover}\:{Z}^{\mathrm{4}} =\mathrm{2}−\mathrm{2}{i} \\ $$
Answered by mathmax by abdo last updated on 07/Feb/21
![2−2i =2(1−i) =2(√2)((1/( (√2)))−(i/( (√2))))=2(√2)e^(−((iπ)/4)) =2^(3/2) e^(−((iπ)/4)) let Z =re^(iθ) e⇒r^4 e^(i4θ) =2^(3/2) .e^(i(−(π/4)+2kπ)) ⇒r=2^(3/8) and4θ =−(π/4)+2kπ ⇒ r =^8 (√8) and θ_k =−(π/(16))+((kπ)/2) with k∈[[0,3]] so the roots are Z_k =^8 (√8)e^(i(−(π/(16))+((kπ)/2))) and k∈{o,1,2,3}](https://www.tinkutara.com/question/Q131736.png)
$$\mathrm{2}−\mathrm{2i}\:=\mathrm{2}\left(\mathrm{1}−\mathrm{i}\right)\:=\mathrm{2}\sqrt{\mathrm{2}}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\frac{\mathrm{i}}{\:\sqrt{\mathrm{2}}}\right)=\mathrm{2}\sqrt{\mathrm{2}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \:=\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{2}}} \:\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \\ $$$$\mathrm{let}\:\mathrm{Z}\:=\mathrm{re}^{\mathrm{i}\theta} \:\:\mathrm{e}\Rightarrow\mathrm{r}^{\mathrm{4}} \:\mathrm{e}^{\mathrm{i4}\theta} \:=\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{2}}} .\mathrm{e}^{\mathrm{i}\left(−\frac{\pi}{\mathrm{4}}+\mathrm{2k}\pi\right)} \:\Rightarrow\mathrm{r}=\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{8}}} \:\mathrm{and4}\theta\:=−\frac{\pi}{\mathrm{4}}+\mathrm{2k}\pi\:\Rightarrow \\ $$$$\mathrm{r}\:=^{\mathrm{8}} \sqrt{\mathrm{8}}\:\mathrm{and}\:\theta_{\mathrm{k}} =−\frac{\pi}{\mathrm{16}}+\frac{\mathrm{k}\pi}{\mathrm{2}}\:\:\mathrm{with}\:\mathrm{k}\in\left[\left[\mathrm{0},\mathrm{3}\right]\right]\:\mathrm{so}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{are} \\ $$$$\mathrm{Z}_{\mathrm{k}} =^{\mathrm{8}} \sqrt{\mathrm{8}}\mathrm{e}^{\mathrm{i}\left(−\frac{\pi}{\mathrm{16}}+\frac{\mathrm{k}\pi}{\mathrm{2}}\right)} \:\:\mathrm{and}\:\mathrm{k}\in\left\{\mathrm{o},\mathrm{1},\mathrm{2},\mathrm{3}\right\} \\ $$
Answered by mr W last updated on 07/Feb/21
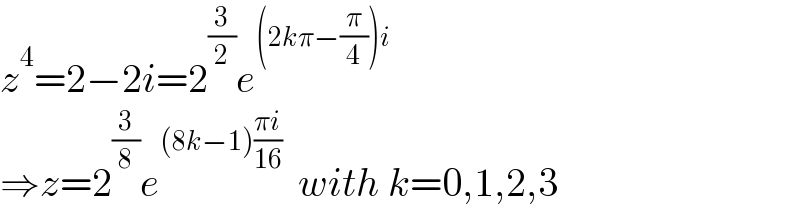
$${z}^{\mathrm{4}} =\mathrm{2}−\mathrm{2}{i}=\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{2}}} {e}^{\left(\mathrm{2}{k}\pi−\frac{\pi}{\mathrm{4}}\right){i}} \\ $$$$\Rightarrow{z}=\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{8}}} {e}^{\left(\mathrm{8}{k}−\mathrm{1}\right)\frac{\pi{i}}{\mathrm{16}}} \:\:{with}\:{k}=\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3} \\ $$
