Question Number 68935 by Maclaurin Stickker last updated on 17/Sep/19
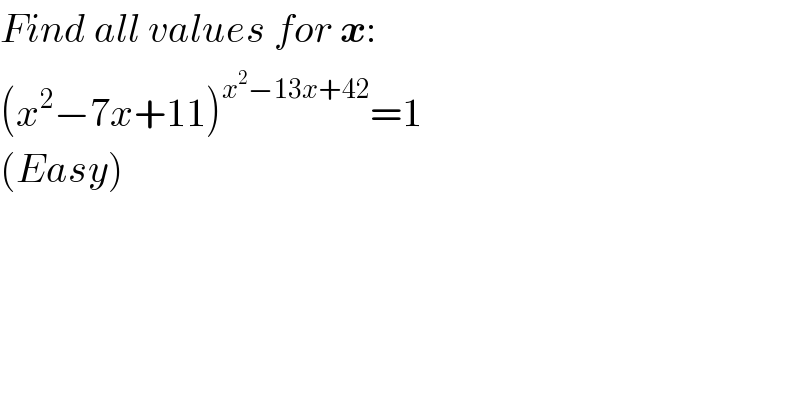
$${Find}\:{all}\:{values}\:{for}\:\boldsymbol{{x}}: \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{11}\right)^{{x}^{\mathrm{2}} −\mathrm{13}{x}+\mathrm{42}} =\mathrm{1} \\ $$$$\left({Easy}\right) \\ $$
Answered by $@ty@m123 last updated on 17/Sep/19
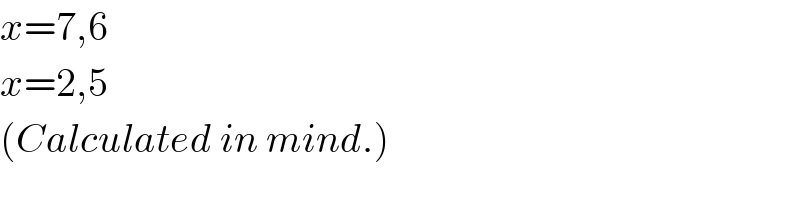
$${x}=\mathrm{7},\mathrm{6} \\ $$$${x}=\mathrm{2},\mathrm{5} \\ $$$$\left({Calculated}\:{in}\:{mind}.\right) \\ $$
Answered by Rasheed.Sindhi last updated on 17/Sep/19
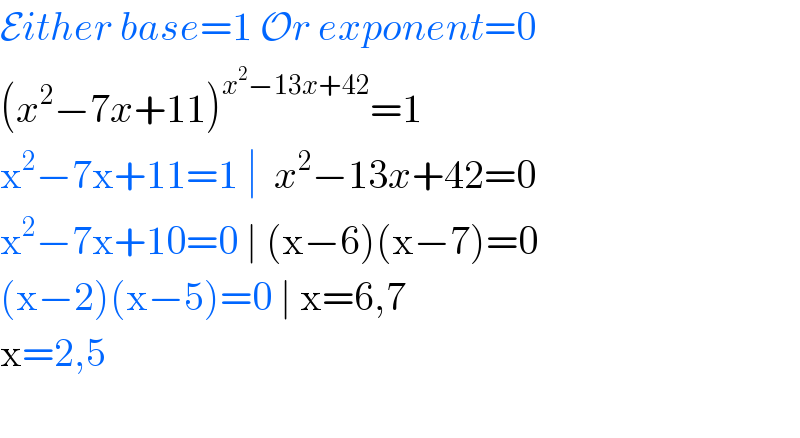
$$\mathcal{E}{ither}\:{base}=\mathrm{1}\:\mathcal{O}{r}\:{exponent}=\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{11}\right)^{{x}^{\mathrm{2}} −\mathrm{13}{x}+\mathrm{42}} =\mathrm{1} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{7x}+\mathrm{11}=\mathrm{1}\:\mid\:\:{x}^{\mathrm{2}} −\mathrm{13}{x}+\mathrm{42}=\mathrm{0} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{7x}+\mathrm{10}=\mathrm{0}\:\mid\:\left(\mathrm{x}−\mathrm{6}\right)\left(\mathrm{x}−\mathrm{7}\right)=\mathrm{0} \\ $$$$\left(\mathrm{x}−\mathrm{2}\right)\left(\mathrm{x}−\mathrm{5}\right)=\mathrm{0}\:\mid\:\mathrm{x}=\mathrm{6},\mathrm{7} \\ $$$$\mathrm{x}=\mathrm{2},\mathrm{5} \\ $$$$ \\ $$
