Question Number 74582 by Maclaurin Stickker last updated on 26/Nov/19
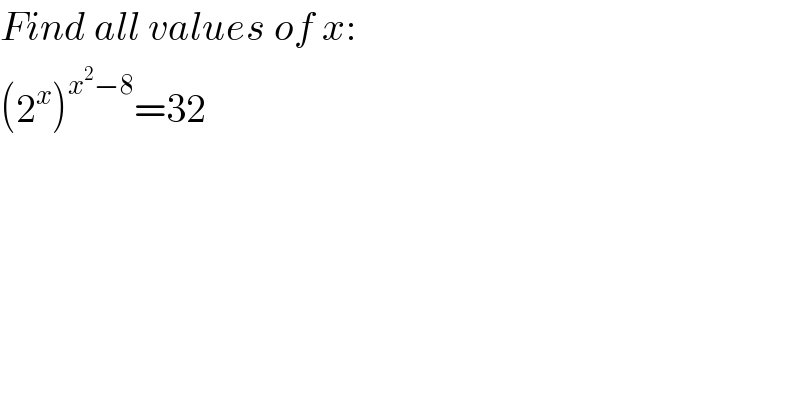
$${Find}\:{all}\:{values}\:{of}\:{x}: \\ $$$$\left(\mathrm{2}^{{x}} \right)^{{x}^{\mathrm{2}} −\mathrm{8}} =\mathrm{32} \\ $$
Answered by MJS last updated on 26/Nov/19

$$\left({a}^{{b}} \right)^{{c}} ={a}^{{bc}} \\ $$$$\mathrm{2}^{{x}^{\mathrm{3}} −\mathrm{8}{x}} =\mathrm{2}^{\mathrm{5}} \\ $$$${x}^{\mathrm{3}} −\mathrm{8}{x}−\mathrm{5}=\mathrm{0} \\ $$$$\mathrm{this}\:\mathrm{has}\:\mathrm{3}\:\mathrm{real}\:\mathrm{solutions}\:\Rightarrow\:\mathrm{we}\:\mathrm{need}\:\mathrm{the} \\ $$$$\mathrm{trigonometric}\:\mathrm{formula} \\ $$$${x}_{\mathrm{1}} =\frac{\mathrm{4}\sqrt{\mathrm{6}}}{\mathrm{3}}\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{\mathrm{15}\sqrt{\mathrm{6}}}{\mathrm{64}}\right)\:\approx\mathrm{3}.\mathrm{10043} \\ $$$${x}_{\mathrm{2}} =−\frac{\mathrm{4}\sqrt{\mathrm{6}}}{\mathrm{3}}\mathrm{sin}\:\left(\frac{\pi}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{\mathrm{15}\sqrt{\mathrm{6}}}{\mathrm{64}}\right)\:\approx−\mathrm{2}.\mathrm{43931} \\ $$$${x}_{\mathrm{3}} =−\frac{\mathrm{4}\sqrt{\mathrm{6}}}{\mathrm{3}}\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{\mathrm{15}\sqrt{\mathrm{6}}}{\mathrm{64}}\right)\:\approx−.\mathrm{661120} \\ $$
