Menu Close

Find-at-least-the-first-four-non-zero-term-in-a-power-series-expansion-about-x-0-for-a-general-solution-to-z-x-2-z-0-

Tinku Tara 0 Comments
Pin




Question Number 71761 by TawaTawa last updated on 19/Oct/19
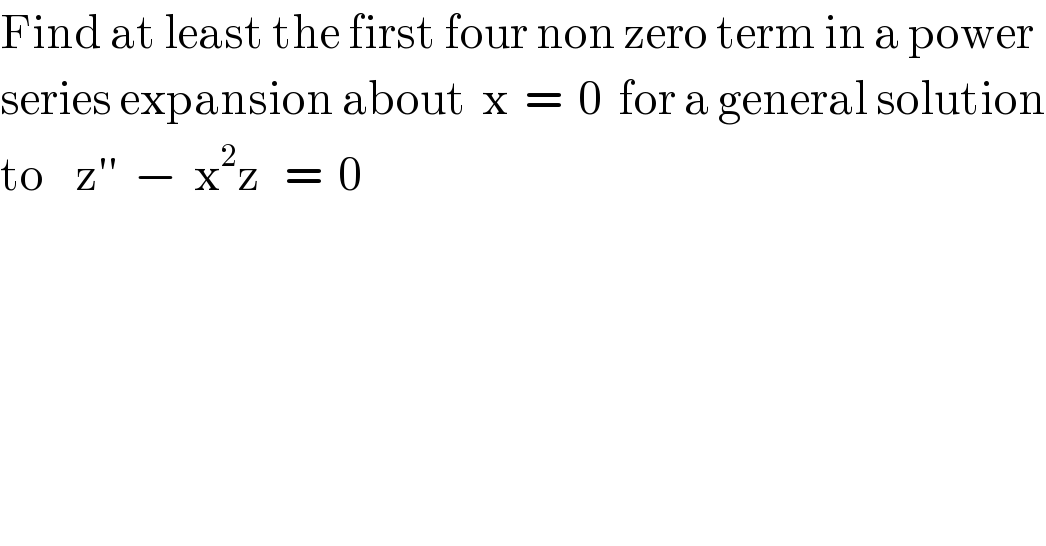
Find at least the first four non zero term in a power series expansion about x = 0 for a general solution to z′′ − x^2 z = 0
$$\mathrm{Find}\:\mathrm{at}\:\mathrm{least}\:\mathrm{the}\:\mathrm{first}\:\mathrm{four}\:\mathrm{non}\:\mathrm{zero}\:\mathrm{term}\:\mathrm{in}\:\mathrm{a}\:\mathrm{power} \\ $$$$\mathrm{series}\:\mathrm{expansion}\:\mathrm{about}\:\:\mathrm{x}\:\:=\:\:\mathrm{0}\:\:\mathrm{for}\:\mathrm{a}\:\mathrm{general}\:\mathrm{solution} \\ $$$$\mathrm{to}\:\:\:\:\mathrm{z}''\:\:−\:\:\mathrm{x}^{\mathrm{2}} \mathrm{z}\:\:\:=\:\:\mathrm{0} \\ $$
Commented by mathmax by abdo last updated on 19/Oct/19
let z =Σ_(n=0) ^∞ a_n x^n ⇒z^′ =Σ_(n=1) ^∞ na_n x^(n−1) and z^(′′) =Σ_(n=2) ^∞ n(n−1)a_n x^(n−2) (e)⇒Σ_(n=2) ^∞ n_((ch. n−2=k)) (n−1)a_n x^(n−2) −x^2 Σ_(n=0) ^∞ a_n x^n =0 ⇒ =Σ_(k=0) ^∞ (k+2)(k+1)a_(k+2) x^k −Σ_(k=0(ch.k+2=n)) ^∞ a_k x^(k+2) =0 ⇒ Σ_(k=0) ^∞ (k+1)(k+2)a_(k+2) x^k −Σ_(n=2) ^∞ a_(n−2) x^n =0 ⇒ 2a_2 +6a_3 x +Σ_(n=2) ^∞ {(n+1)(n+2)a_(n+2) −a_(n−2) }x^n =0 ⇒a_2 =a_3 =0 and ∀n≥2 (n+1)(n+2)a_(n+2) −a_(n−2) =0 ⇒∀n≥2 a_(n+2) =(a_(n−2) /((n+1)(n+2))) ⇒a_2 =(a_0 /(1×2))=0 ⇒a_0 =0 a_3 =(a_1 /(2×6)) =0 ⇒a_1 =0 we have a_(2n+2) =(a_(2n) /((2n+1)(2n+2))) and a_(2n+3) =(a_(2n−1) /((2n+2)(2n+3)))
$${let}\:{z}\:=\sum_{{n}=\mathrm{0}} ^{\infty} {a}_{{n}} {x}^{{n}} \:\Rightarrow{z}^{'} =\sum_{{n}=\mathrm{1}} ^{\infty} {na}_{{n}} {x}^{{n}−\mathrm{1}} \:{and}\:{z}^{''} =\sum_{{n}=\mathrm{2}} ^{\infty} {n}\left({n}−\mathrm{1}\right){a}_{{n}} {x}^{{n}−\mathrm{2}} \\ $$$$\left({e}\right)\Rightarrow\sum_{{n}=\mathrm{2}} ^{\infty} {n}_{\left({ch}.\:{n}−\mathrm{2}={k}\right)} \left({n}−\mathrm{1}\right){a}_{{n}} {x}^{{n}−\mathrm{2}} −{x}^{\mathrm{2}} \sum_{{n}=\mathrm{0}} ^{\infty} \:{a}_{{n}} {x}^{{n}} =\mathrm{0}\:\Rightarrow \\ $$$$=\sum_{{k}=\mathrm{0}} ^{\infty} \left({k}+\mathrm{2}\right)\left({k}+\mathrm{1}\right){a}_{{k}+\mathrm{2}} {x}^{{k}} −\sum_{{k}=\mathrm{0}\left({ch}.{k}+\mathrm{2}={n}\right)} ^{\infty} \:{a}_{{k}} {x}^{{k}+\mathrm{2}} =\mathrm{0}\:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{0}} ^{\infty} \left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right){a}_{{k}+\mathrm{2}} {x}^{{k}} −\sum_{{n}=\mathrm{2}} ^{\infty} \:{a}_{{n}−\mathrm{2}} {x}^{{n}} \:=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{2}{a}_{\mathrm{2}} \:+\mathrm{6}{a}_{\mathrm{3}} {x}\:+\sum_{{n}=\mathrm{2}} ^{\infty} \left\{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right){a}_{{n}+\mathrm{2}} −{a}_{{n}−\mathrm{2}} \right\}{x}^{{n}} \:=\mathrm{0}\:\Rightarrow{a}_{\mathrm{2}} ={a}_{\mathrm{3}} =\mathrm{0}\:{and} \\ $$$$\forall{n}\geqslant\mathrm{2}\:\:\:\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right){a}_{{n}+\mathrm{2}} −{a}_{{n}−\mathrm{2}} =\mathrm{0}\:\Rightarrow\forall{n}\geqslant\mathrm{2}\: \\ $$$${a}_{{n}+\mathrm{2}} =\frac{{a}_{{n}−\mathrm{2}} }{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}\:\Rightarrow{a}_{\mathrm{2}} =\frac{{a}_{\mathrm{0}} }{\mathrm{1}×\mathrm{2}}=\mathrm{0}\:\Rightarrow{a}_{\mathrm{0}} =\mathrm{0} \\ $$$${a}_{\mathrm{3}} =\frac{{a}_{\mathrm{1}} }{\mathrm{2}×\mathrm{6}}\:=\mathrm{0}\:\Rightarrow{a}_{\mathrm{1}} =\mathrm{0} \\ $$$${we}\:{have}\:{a}_{\mathrm{2}{n}+\mathrm{2}} =\frac{{a}_{\mathrm{2}{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{2}\right)}\:{and} \\ $$$${a}_{\mathrm{2}{n}+\mathrm{3}} =\frac{{a}_{\mathrm{2}{n}−\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{2}\right)\left(\mathrm{2}{n}+\mathrm{3}\right)} \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 19/Oct/19
we have (a_(2n+2) /a_(2n) ) =(1/(2(n+1)(2n+1))) ⇒ Π_(k=2) ^n (a_(2k+2) /a_(2k) ) =(1/2^(n−2) )×Π_(k=2) ^n (1/((k+1)(2k+1))) ⇒ (a_6 /a_4 ).(a_8 /a_6 )......(a_(2n+2) /a_(2n) ) =(1/2^(n−2) )×Π_(k=2) ^n (1/(k+1))Π_(k=2) ^n (1/(2k+1)) =(1/2^(n−2) )×(1/(3.4....(n+1)))×(1/(5.7.....(2n+1))) =(2/2^(n−2) )×(1/((n+1)!)) ×((3.2.6.....(2n))/(2.3.5.6.7.....(2n)(2n+1))) =(2/(2^(n−2) (n+1)!))×((3. 2^n n!)/((2n+1)!)) =2^(n+1−n+2) ×((n!)/((n+1)!(2n+1)!)) =((8n!)/((n+1)!(2n+1)!)) ....
$${we}\:{have}\:\frac{{a}_{\mathrm{2}{n}+\mathrm{2}} }{{a}_{\mathrm{2}{n}} }\:=\frac{\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}\:\Rightarrow \\ $$$$\prod_{{k}=\mathrm{2}} ^{{n}} \:\:\frac{{a}_{\mathrm{2}{k}+\mathrm{2}} }{{a}_{\mathrm{2}{k}} }\:=\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{2}} }×\prod_{{k}=\mathrm{2}} ^{{n}} \:\:\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)}\:\Rightarrow \\ $$$$\frac{{a}_{\mathrm{6}} }{{a}_{\mathrm{4}} }.\frac{{a}_{\mathrm{8}} }{{a}_{\mathrm{6}} }……\frac{{a}_{\mathrm{2}{n}+\mathrm{2}} }{{a}_{\mathrm{2}{n}} }\:=\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{2}} }×\prod_{{k}=\mathrm{2}} ^{{n}} \:\frac{\mathrm{1}}{{k}+\mathrm{1}}\prod_{{k}=\mathrm{2}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{2}} }×\frac{\mathrm{1}}{\mathrm{3}.\mathrm{4}….\left({n}+\mathrm{1}\right)}×\frac{\mathrm{1}}{\mathrm{5}.\mathrm{7}…..\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{2}}{\mathrm{2}^{{n}−\mathrm{2}} }×\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)!}\:×\frac{\mathrm{3}.\mathrm{2}.\mathrm{6}…..\left(\mathrm{2}{n}\right)}{\mathrm{2}.\mathrm{3}.\mathrm{5}.\mathrm{6}.\mathrm{7}…..\left(\mathrm{2}{n}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{2}}{\mathrm{2}^{{n}−\mathrm{2}} \left({n}+\mathrm{1}\right)!}×\frac{\mathrm{3}.\:\mathrm{2}^{{n}} {n}!}{\left(\mathrm{2}{n}+\mathrm{1}\right)!}\:=\mathrm{2}^{{n}+\mathrm{1}−{n}+\mathrm{2}} ×\frac{{n}!}{\left({n}+\mathrm{1}\right)!\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$$$=\frac{\mathrm{8}{n}!}{\left({n}+\mathrm{1}\right)!\left(\mathrm{2}{n}+\mathrm{1}\right)!}\:…. \\ $$
Commented by TawaTawa last updated on 19/Oct/19
God bless you sir. Thanks for your time
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time} \\ $$
Commented by mathmax by abdo last updated on 20/Oct/19
you are welcome.
$${you}\:{are}\:{welcome}. \\ $$
Commented by TawaTawa last updated on 23/Oct/19
Sir, will i just put values of n = 1, 2, 3, 4, .... to find the least first four term ?
$$\mathrm{Sir},\:\:\mathrm{will}\:\mathrm{i}\:\mathrm{just}\:\mathrm{put}\:\mathrm{values}\:\mathrm{of}\:\:\:\mathrm{n}\:\:=\:\:\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:\mathrm{4},\:\:…. \\ $$$$\mathrm{to}\:\mathrm{find}\:\mathrm{the}\:\mathrm{least}\:\mathrm{first}\:\mathrm{four}\:\mathrm{term}\:? \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *