find-by-recurrence-J-n-p-0-1-x-n-arctanx-p-dx-stydy-the-serie-n-0-and-p-0-J-n-p-

Tinku Tara June 3, 2023 Relation and Functions 0 Comments

Question Number 78280 by msup trace by abdo last updated on 15/Jan/20

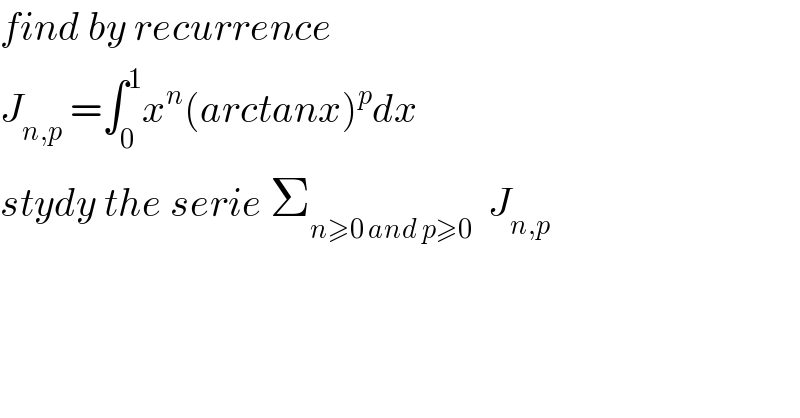
find by recurrence J_(n,p) =∫_0 ^1 x^n (arctanx)^p dx stydy the serie Σ_(n≥0 and p≥0) J_(n,p)

$${find}\:{by}\:{recurrence} \\ $$$${J}_{{n},{p}} \:=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} \left({arctanx}\right)^{{p}} {dx} \\ $$$${stydy}\:{the}\:{serie}\:\sum_{{n}\geqslant\mathrm{0}\:{and}\:{p}\geqslant\mathrm{0}} \:\:{J}_{{n},{p}} \\ $$

Facebook Tweet Pin

find-by-recurrence-J-n-p-0-1-x-n-arctanx-p-dx-stydy-the-serie-n-0-and-p-0-J-n-p-

Leave a Reply Cancel reply