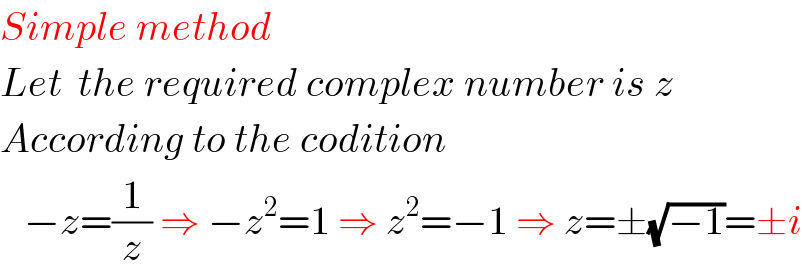Menu Close

Find-complex-number-whose-additive-inverse-is-equal-to-its-multiplicative-inverse-

Tinku Tara 0 Comments
Pin




Question Number 6512 by Rasheed Soomro last updated on 30/Jun/16
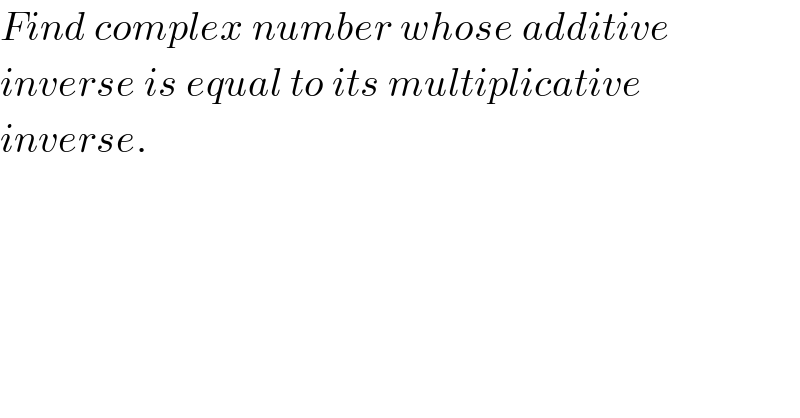
Find complex number whose additive inverse is equal to its multiplicative inverse.
Findcomplexnumberwhoseadditiveinverseisequaltoitsmultiplicativeinverse.
Commented by Temp last updated on 30/Jun/16
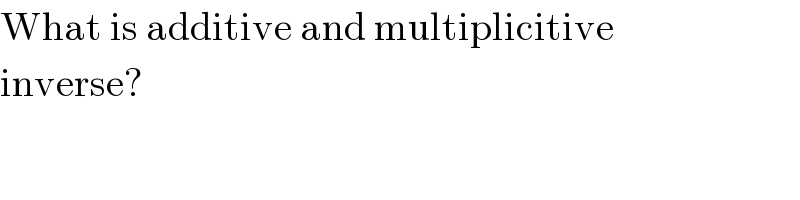
What is additive and multiplicitive inverse?
Whatisadditiveandmultiplicitiveinverse?
Commented by Rasheed Soomro last updated on 30/Jun/16
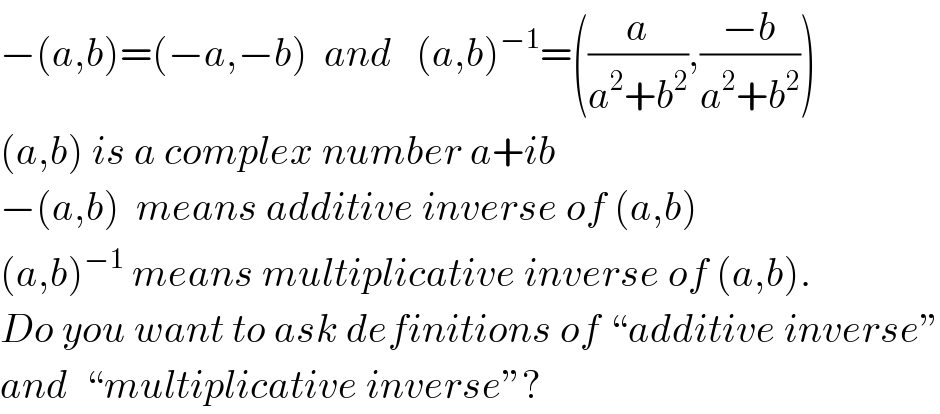
−(a,b)=(−a,−b) and (a,b)^(−1) =((a/(a^2 +b^2 )),((−b)/(a^2 +b^2 ))) (a,b) is a complex number a+ib −(a,b) means additive inverse of (a,b) (a,b)^(−1) means multiplicative inverse of (a,b). Do you want to ask definitions of “additive inverse” and “multiplicative inverse”?
−(a,b)=(−a,−b)and(a,b)−1=(aa2+b2,−ba2+b2)(a,b)isacomplexnumbera+ib−(a,b)meansadditiveinverseof(a,b)(a,b)−1meansmultiplicativeinverseof(a,b).Doyouwanttoaskdefinitionsof“additiveinverse″and“multiplicativeinverse″?
Answered by Yozzii last updated on 30/Jun/16
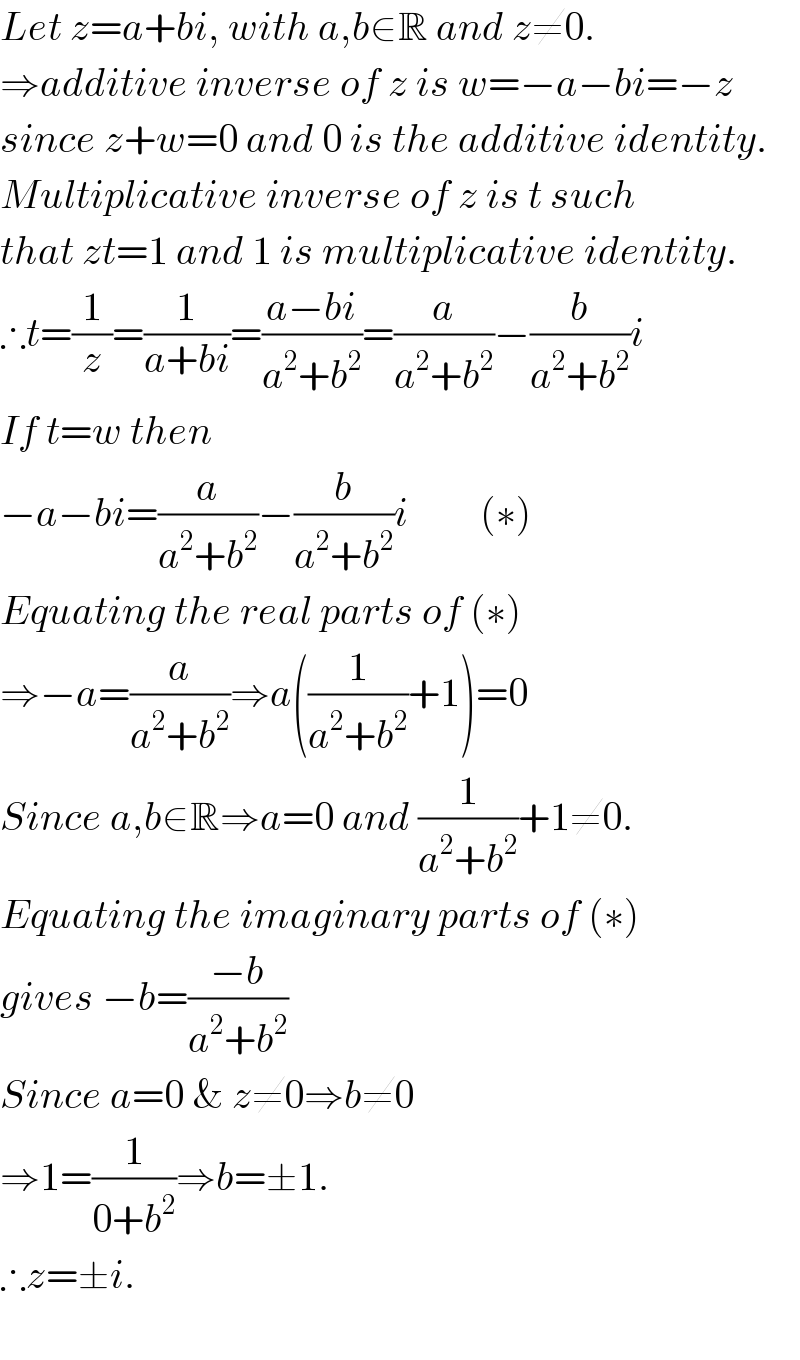
Let z=a+bi, with a,b∈R and z≠0. ⇒additive inverse of z is w=−a−bi=−z since z+w=0 and 0 is the additive identity. Multiplicative inverse of z is t such that zt=1 and 1 is multiplicative identity. ∴t=(1/z)=(1/(a+bi))=((a−bi)/(a^2 +b^2 ))=(a/(a^2 +b^2 ))−(b/(a^2 +b^2 ))i If t=w then −a−bi=(a/(a^2 +b^2 ))−(b/(a^2 +b^2 ))i (∗) Equating the real parts of (∗) ⇒−a=(a/(a^2 +b^2 ))⇒a((1/(a^2 +b^2 ))+1)=0 Since a,b∈R⇒a=0 and (1/(a^2 +b^2 ))+1≠0. Equating the imaginary parts of (∗) gives −b=((−b)/(a^2 +b^2 )) Since a=0 & z≠0⇒b≠0 ⇒1=(1/(0+b^2 ))⇒b=±1. ∴z=±i.
Letz=a+bi,witha,b∈Randz≠0.⇒additiveinverseofzisw=−a−bi=−zsincez+w=0and0istheadditiveidentity.Multiplicativeinverseofzistsuchthatzt=1and1ismultiplicativeidentity.∴t=1z=1a+bi=a−bia2+b2=aa2+b2−ba2+b2iIft=wthen−a−bi=aa2+b2−ba2+b2i(∗)Equatingtherealpartsof(∗)⇒−a=aa2+b2⇒a(1a2+b2+1)=0Sincea,b∈R⇒a=0and1a2+b2+1≠0.Equatingtheimaginarypartsof(∗)gives−b=−ba2+b2Sincea=0&z≠0⇒b≠0⇒1=10+b2⇒b=±1.∴z=±i.
Commented by Rasheed Soomro last updated on 30/Jun/16
THαnX!
THαnX!
Answered by Rasheed Soomro last updated on 01/Jul/16
Simple method Let the required complex number is z According to the codition −z=(1/z) ⇒ −z^2 =1 ⇒ z^2 =−1 ⇒ z=±(√(−1))=±i
SimplemethodLettherequiredcomplexnumberiszAccordingtothecodition−z=1z⇒−z2=1⇒z2=−1⇒z=±−1=±i

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *