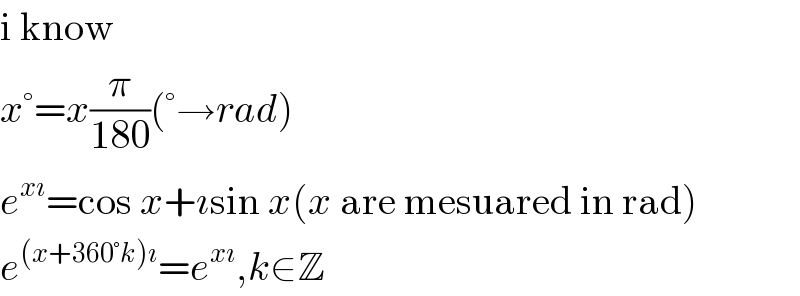Find-complex-numbers-and-such-that-2-3-and-2-3-

Question Number 1497 by Rasheed Soomro last updated on 14/Aug/15

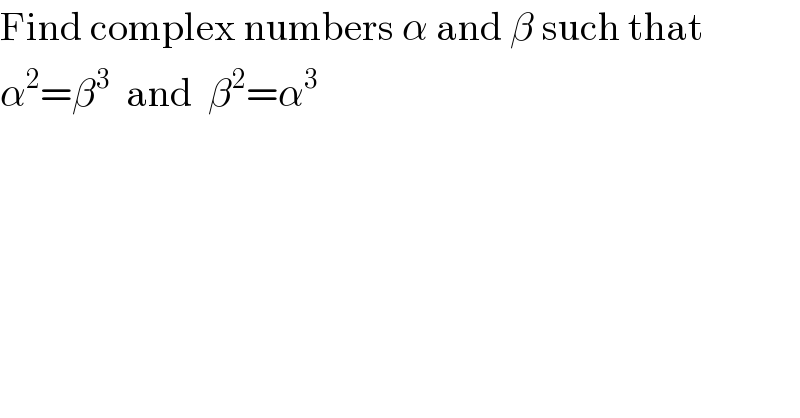
Find complex numbers α and β such that

α^{2} = β^{3} and β^{2} = α^{3}

Commented by 123456 last updated on 14/Aug/15

(α, β) = (0, 0) is ome of these pairs

Commented by Rasheed Ahmad last updated on 14/Aug/15

(1, 1) i s a n o t h e r p a i r .

Commented by 123456 last updated on 15/Aug/15

{\begin{cases} α^{2} = β^{3} \\ β^{2} = α^{3} \end{cases}

n \in N^{*}

{\begin{cases} α^{4 n} = β^{6 n} \\ β^{6 n} = α^{9 n} \end{cases}

α^{4 n} = α^{9 n} \Leftrightarrow α^{4 n} (α^{5 n} - 1) = 0

{\begin{cases} α^{6 n} = β^{9 n} \\ β^{4 n} = α^{6 n} \end{cases}

β^{4 n} = β^{9 n} \Leftrightarrow β^{4 n} (β^{5 n} - 1) = 0

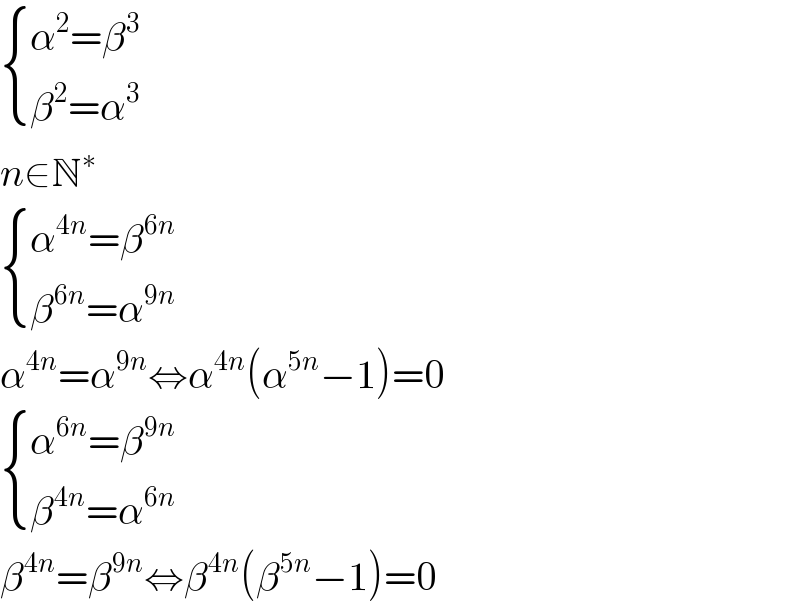
Commented by Rasheed Soomro last updated on 16/Aug/15

α^{2} = β^{3}

{(α^{2})}^{2} = {(β^{3})}^{2}

α^{4} = {(β^{2})}^{3}

α^{4} = {(α^{3})}^{3} [s u b s t i t u t i n g β^{2} = α^{3}]

α^{4} = α^{9}

A s s u m i n g α \neq 0, d i v i d i n g b y α^{4}

α^{5} = 1 \Rightarrow α =^{5} \sqrt{1}

S i m i l a r i l y,

β^{5} = 1 \Rightarrow β =^{5} \sqrt{1}

∴ α a n d β b o t h a r e 5 t h r o o t s o f u n i t y .

W e k n o w t h a t

n t h r o o t o f u n i t y = {(c o s \frac{2 π}{n} + ı s i n \frac{2 π}{n})}^{k}, k = 0, 1, 2, \dots (n - 1)

5 t h r o o t o f u n i t y = {(c o s \frac{2 π}{5} + ı s i n \frac{2 π}{5})}^{k}, k = 0, 1, 2, \dots 4

L e t c o s \frac{2 π}{5} + ı s i n \frac{2 π}{5} = ω

5 t h r o o t o f u n i t y = 1, ω, ω^{2}, ω^{3}, ω^{4} (i n o r d e r)

S q u a r e o f ∽ = 1, ω^{2}, ω^{4}, ω, ω^{3} (i n o r d e r)

C u b e o f ∽ = 1, w^{3}, ω, ω^{4}, ω^{2} (i n o r d e r)

{(ω^{k_{1}})}^{2} = {(ω^{k_{2}})}^{3} k_{1}, k_{2} = 0, 1, 2, 3, 4

ω^{2 k_{1} (m o d 5)} = ω^{3 k_{2} (m o d 5)}

F o r 2 k_{1} (m o d 5) = 3 k_{2} (m o d 5) :

(α, β) = (ω^{k_{1}}, ω^{k_{2}}) = (ω^{k_{2}}, ω^{k_{1}})

(α, β) = {(1, 1), (ω, ω^{4}), (ω^{4}, ω), (ω^{2}, ω^{3}), (ω^{3}, ω^{2})}

Commented by 123456 last updated on 15/Aug/15

good approach :)

Commented by Rasheed Soomro last updated on 16/Aug/15

Thanks . Please comment, although in negative, o n m y

a n s w e r s t o Q - 1448 a n d Q - 1466 . I f t h e c o m m e n t s b e

p o s i t i v e I w i l l g a i n c o n f i d e n c e a n d i f t h e y a r e n e g a t i v e

I w i l l l e a r n s o m e t h i n g . S o p l e a s e \dots . .

Answered by 123456 last updated on 15/Aug/15

{\begin{cases} α^{2} = β^{3} \\ β^{2} = α^{3} \end{cases} \Rightarrow {\begin{cases} α^{4} = β^{6} \\ β^{6} = α^{9} \end{cases}

α^{4} = α^{9}

α^{9} - α^{4} = 0

α^{4} (α^{5} - 1) = 0

α = 0 \lor α = \sqrt[5]{1}

α = 0 \Rightarrow {\begin{cases} β^{3} = 0 \\ β^{2} = 0 \end{cases} \Rightarrow β = 0

α = 1 \Rightarrow {\begin{cases} β^{3} = 1 \\ β^{2} = 1 \end{cases} \Rightarrow {\begin{cases} β = 1 \lor β = - \frac{1}{2} + \frac{\sqrt{3}}{2} ı \lor β = - \frac{1}{2} - \frac{\sqrt{3}}{2} ı \\ β = 1 \lor β = - 1 \end{cases} \Rightarrow β = 1

α = e^{72 ° ı} \Rightarrow {\begin{cases} β^{3} = e^{144 ° ı} \\ β^{2} = e^{216 ° ı} \end{cases} \Rightarrow {\begin{cases} β = e^{48 ° ı} \lor β = e^{168 ° ı} \lor β = e^{288 ° ı} \\ β = e^{108 ° ı} \lor β = e^{288 ° ı} \end{cases} \Rightarrow β = e^{288 ° ı}

α = e^{144 ° ı} \Rightarrow {\begin{cases} β^{3} = e^{288 ° ı} \\ β^{2} = e^{72 ° ı} \end{cases} \Rightarrow {\begin{cases} β = e^{96 ° ı} \lor β = e^{216 ° ı} \lor β = e^{336 ° ı} \\ β = e^{36 ° ı} \lor β = e^{216 ° ı} \end{cases} \Rightarrow β = e^{216 ° ı}

α = e^{216 ° ı} \Rightarrow {\begin{cases} β^{3} = e^{72 ° ı} \\ β^{2} = e^{288 ° ı} \end{cases} \Rightarrow {\begin{cases} β = e^{24 ° ı} \lor β = e^{144 ° ı} \lor β = e^{264 ° ı} \\ β = e^{144 ° ı} \lor β = e^{324 ° ı} \end{cases}

α = e^{288 ° ı} \Rightarrow {\begin{cases} β^{3} = e^{216 ° ı} \\ β^{2} = e^{144 ° ı} \end{cases} \Rightarrow {\begin{cases} β = e^{72 ° ı} \lor β = e^{192 ° ı} \lor β = e^{312 ° ı} \\ β = e^{72 ° ı} \lor β = e^{252 ° ı} \end{cases} \Rightarrow β = e^{72 ° ı}

S = {(0, 0), (1, 1), (e^{72 ° ı}, e^{288 ° ı}), (e^{144 ° ı}, e^{216 ° ı}), (e^{216 ° ı}, e^{144 ° ı}), (e^{288 ° ı}, e^{72 ° ı})}

Commented by Rasheed Ahmad last updated on 15/Aug/15

(R a s h e e d S o o m r o)

Excellent Sir!

Commented by 123456 last updated on 15/Aug/15

i know

x ° = x \frac{π}{180} (° \to r a d)

e^{x ı} = \cos x + ı \sin x (x are mesuared in rad)

e^{(x + 360 ° k) ı} = e^{x ı}, k \in Z

Facebook Tweet Pin