Question Number 1498 by Rasheed Soomro last updated on 14/Aug/15

$$\mathrm{Find}\:\mathrm{complex}\:\mathrm{numbers}\:\alpha\:{and}\:\:\beta\:\:\mathrm{such}\:\mathrm{that} \\ $$$$\alpha^{\:{m}} =\beta^{\:\:{n}} \:\:\:\:{and}\:\:\:\beta^{\:\:{m}} =\alpha^{\mathrm{n}} \:\:,\:{m},{n}\:\in\:\mathbb{Z} \\ $$$$\boldsymbol{\mathrm{D}}\mathrm{etermine}\:\mathrm{formula}\:\mathrm{for}\:\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{pairs}\:\left(\alpha,\beta\right)\:\mathrm{fulfilling}\:\mathrm{the} \\ $$$$\mathrm{above}\:\mathrm{conditions}.\:\:\left(\:\mathrm{You}\:\mathrm{may}\:\mathrm{ignore}\:\mathrm{this}\:\mathrm{part}\:\mathrm{in}\:\mathrm{your}\:\mathrm{answer}\right) \\ $$
Commented by 123456 last updated on 14/Aug/15
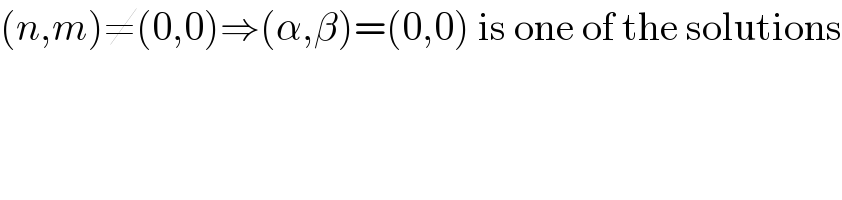
$$\left({n},{m}\right)\neq\left(\mathrm{0},\mathrm{0}\right)\Rightarrow\left(\alpha,\beta\right)=\left(\mathrm{0},\mathrm{0}\right)\:\mathrm{is}\:\mathrm{one}\:\mathrm{of}\:\mathrm{the}\:\mathrm{solutions} \\ $$
Commented by Rasheed Ahmad last updated on 14/Aug/15
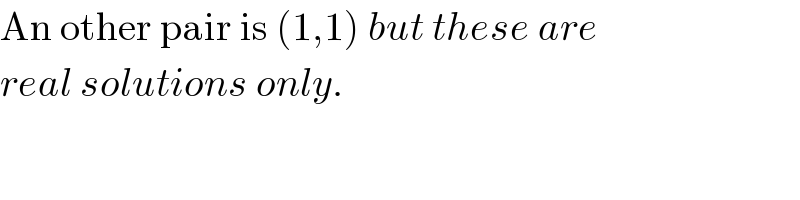
$$\mathrm{An}\:\mathrm{other}\:\mathrm{pair}\:\mathrm{is}\:\left(\mathrm{1},\mathrm{1}\right)\:{but}\:{these}\:{are} \\ $$$${real}\:{solutions}\:{only}. \\ $$
Commented by 123456 last updated on 15/Aug/15
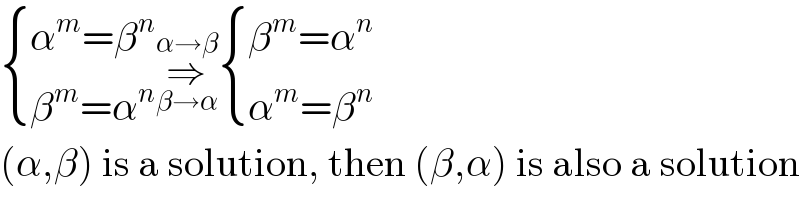
$$\begin{cases}{\alpha^{{m}} =\beta^{{n}} }\\{\beta^{{m}} =\alpha^{{n}} }\end{cases}\underset{\beta\rightarrow\alpha} {\overset{\alpha\rightarrow\beta} {\Rightarrow}}\begin{cases}{\beta^{{m}} =\alpha^{{n}} }\\{\alpha^{{m}} =\beta^{{n}} }\end{cases} \\ $$$$\left(\alpha,\beta\right)\:\mathrm{is}\:\mathrm{a}\:\mathrm{solution},\:\mathrm{then}\:\left(\beta,\alpha\right)\:\mathrm{is}\:\mathrm{also}\:\mathrm{a}\:\mathrm{solution} \\ $$
Commented by Rasheed Ahmad last updated on 15/Aug/15

$$\mathrm{Good}\:\mathrm{deduction}! \\ $$
Commented by 123456 last updated on 15/Aug/15
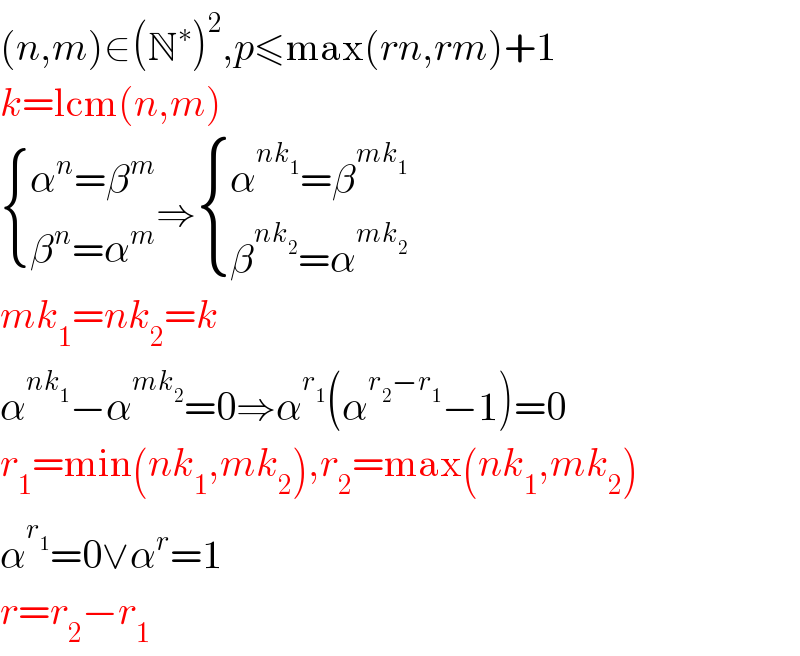
$$\left({n},{m}\right)\in\left(\mathbb{N}^{\ast} \right)^{\mathrm{2}} ,{p}\leqslant\mathrm{max}\left({rn},{rm}\right)+\mathrm{1} \\ $$$${k}=\mathrm{lcm}\left({n},{m}\right) \\ $$$$\begin{cases}{\alpha^{{n}} =\beta^{{m}} }\\{\beta^{{n}} =\alpha^{{m}} }\end{cases}\Rightarrow\begin{cases}{\alpha^{{nk}_{\mathrm{1}} } =\beta^{{mk}_{\mathrm{1}} } }\\{\beta^{{nk}_{\mathrm{2}} } =\alpha^{{mk}_{\mathrm{2}} } }\end{cases} \\ $$$${mk}_{\mathrm{1}} ={nk}_{\mathrm{2}} ={k} \\ $$$$\alpha^{{nk}_{\mathrm{1}} } −\alpha^{{mk}_{\mathrm{2}} } =\mathrm{0}\Rightarrow\alpha^{{r}_{\mathrm{1}} } \left(\alpha^{{r}_{\mathrm{2}} −{r}_{\mathrm{1}} } −\mathrm{1}\right)=\mathrm{0} \\ $$$${r}_{\mathrm{1}} =\mathrm{min}\left({nk}_{\mathrm{1}} ,{mk}_{\mathrm{2}} \right),{r}_{\mathrm{2}} =\mathrm{max}\left({nk}_{\mathrm{1}} ,{mk}_{\mathrm{2}} \right) \\ $$$$\alpha^{{r}_{\mathrm{1}} } =\mathrm{0}\vee\alpha^{{r}} =\mathrm{1} \\ $$$${r}={r}_{\mathrm{2}} −{r}_{\mathrm{1}} \\ $$
Commented by Rasheed Soomro last updated on 15/Aug/15
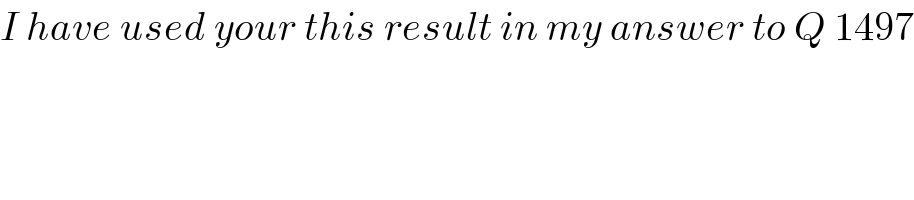
$${I}\:{have}\:{used}\:{your}\:{this}\:{result}\:{in}\:{my}\:{answer}\:{to}\:{Q}\:\mathrm{1497} \\ $$
Answered by Rasheed Soomro last updated on 17/Aug/15
![Let gcd(m,n)=k ⇒ lcm(m,n)=((mn)/k) α^m =β^( n) ⇒( α^m )^(m/k) =(β^( n) )^(m/k) ⇒ α^(m^2 /k) =β^((mn)/k) (I) β^( m) =α^( n) ⇒ (β^( m) )^(n/k) = (α^n )^(n/k) ⇒ β^((mn)/k) =α^(n^2 /k) (II) Our goal is to achieve β ′s common exponent ( of course least common exponent (((mn)/k) ) is suitable for simplified solution) in order to eliminate β in above steps. From (I) and (II) α^(m^2 /k) = α^(n^2 /k) As m and n are exchangeable here we may assume m≥n (If n>m then it will be merely matter of exchanging symbols) α^(m^2 /k) − α^(n^2 /k) =0 ⇒ α^(n^2 /k) ( α^((m^2 /k) − (n^2 /k)) − 1)=0 ⇒ α^(n^2 /k) = 0 ∨ α^((m^2 − n^2 )/k) =1 ⇒ α=0 ∨ α=^((m^2 − n^2 )/k) (√( 1)) (α is (((m^2 − n^2 )/k))th root of unity) α=0 ⇒β=0 [ No need to show process ] ∴ α is (((m^2 − n^2 )/k))th root of unity. Similarly it can be shown that, β is also (((m^2 − n^2 )/k))th root of unity. nth roots of unity are given by: ( cos ((2π)/n) +ı sin ((2π)/n) )^j j=0,1,2,....,n−1 Hence, (((m^2 − n^2 )/k)) th roots of unity will be: ( cos ((2πk)/(m^2 −n^2 )) +ı sin ((2πk)/(m^2 −n^2 )) )^j j=0,1,2,...(.((m^2 − n^2 )/k) −1) Let cos ((2πk)/(m^2 −n^2 )) +ı sin ((2πk)/(m^2 −n^2 )) =ω (((m^2 − n^2 )/k)) th roots of unity=1,ω,ω^2 ,......,ω^((m^2 − n^2 −k)/k) [ Let ((m^2 −n^2 )/k) = N ] mth power of ∽ =1, ω^( m(mod N)) ,ω^( 2m(mod N)) ,...ω^( m(N−1)(mod N)) nth power of ∽ =1, ω^( n(mod N)) ,ω^( 2n(mod N)) ,...ω^( n(N−1)(mod N)) Let j_1 , j_2 =0,1,2,...(.((m^2 − n^2 )/k) −1) Let α = ω^( j_1 ) and β = ω^( j_2 ) are two Nth roots such that α^m =β^( n) ⇒ ω^( mj_1 (mod N)) =ω^( nj_2 (mod N)) ⇒mj_1 (mod N)=nj_2 (mod N) α^n =β^( m) ⇒ ω^( nj_1 (mod N)) =ω^( mj_2 (mod N)) ⇒nj_1 (mod N)=mj_2 (mod N) Therefore −−−−−−−−−−−−−−−−−−−−−−−−− For mj_1 (mod ((m^2 −n^2 )/k) )=nj_2 (mod ((m^2 −n^2 )/k) ) and nj_1 (mod ((m^2 −n^2 )/k) )=mj_2 (mod ((m^2 −n^2 )/k) ) ( α, β)=(ω^j_1 , ω^j_2 )=(ω^j_2 , ω^j_1 ) where ω is (((m^2 − n^2 )/k)) th root of unity( with m≥n).](https://www.tinkutara.com/question/Q1533.png)
$$\:\:\:\:\:\mathrm{Let}\:\mathrm{gcd}\left(\mathrm{m},{n}\right)=\mathrm{k}\:\Rightarrow\:\:\mathrm{lcm}\left(\mathrm{m},{n}\right)=\frac{\mathrm{mn}}{\mathrm{k}} \\ $$$$\alpha^{{m}} =\beta^{\:{n}} \:\Rightarrow\left(\:\alpha^{{m}} \right)^{\frac{\mathrm{m}}{\mathrm{k}}} =\left(\beta^{\:\mathrm{n}} \right)^{\frac{\mathrm{m}}{\mathrm{k}}} \Rightarrow\:\alpha^{\frac{\mathrm{m}^{\mathrm{2}} }{\mathrm{k}}} =\beta^{\frac{\mathrm{mn}}{\mathrm{k}}} \:\:\:\:\:\:\:\:\:\left(\mathrm{I}\right) \\ $$$$\beta^{\:\mathrm{m}} =\alpha^{\:\mathrm{n}} \:\Rightarrow\:\left(\beta^{\:\mathrm{m}} \right)^{\frac{\mathrm{n}}{\mathrm{k}}} =\:\left(\alpha^{\mathrm{n}} \right)^{\frac{\mathrm{n}}{\mathrm{k}}} \Rightarrow\:\beta^{\frac{\mathrm{mn}}{\mathrm{k}}} =\alpha^{\frac{\mathrm{n}^{\mathrm{2}} }{\mathrm{k}}} \:\:\:\:\:\:\:\:\:\left(\mathrm{II}\right) \\ $$$$\mathrm{Our}\:\mathrm{goal}\:\mathrm{is}\:\mathrm{to}\:\mathrm{achieve}\:\beta\:'\mathrm{s}\:\:\mathrm{common}\:\mathrm{exponent}\: \\ $$$$\:\left(\:\mathrm{of}\:\mathrm{course}\:\:\mathrm{least}\:\mathrm{common}\:\mathrm{exponent}\:\left(\frac{\mathrm{mn}}{\mathrm{k}}\:\right)\:\mathrm{is}\:\:\mathrm{suitable}\:\mathrm{for}\:\mathrm{simplified}\:\mathrm{solution}\right)\: \\ $$$$\:\:\:\mathrm{in}\:\mathrm{order}\:\mathrm{to}\:\mathrm{eliminate}\:\beta\:\:\:\mathrm{in}\:\mathrm{above}\:\mathrm{steps}. \\ $$$$ \\ $$$$\mathrm{From}\:\left(\mathrm{I}\right)\:\mathrm{and}\:\left(\mathrm{II}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\alpha^{\frac{\mathrm{m}^{\mathrm{2}} }{\mathrm{k}}} =\:\alpha^{\frac{\mathrm{n}^{\mathrm{2}} }{\mathrm{k}}} \: \\ $$$$\mathrm{As}\:\mathrm{m}\:\mathrm{and}\:\mathrm{n}\:\mathrm{are}\:\mathrm{exchangeable}\:\mathrm{here}\:\mathrm{we}\:\mathrm{may}\:\mathrm{assume}\:\mathrm{m}\geqslant{n}\: \\ $$$$\left(\mathrm{If}\:\mathrm{n}>\mathrm{m}\:\mathrm{then}\:\mathrm{it}\:\mathrm{will}\:\mathrm{be}\:\:\mathrm{merely}\:\mathrm{matter}\:\mathrm{of}\:\mathrm{exchanging}\:\mathrm{symbols}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\alpha^{\frac{\mathrm{m}^{\mathrm{2}} }{\mathrm{k}}} −\:\alpha^{\frac{\mathrm{n}^{\mathrm{2}} }{\mathrm{k}}} \:=\mathrm{0}\:\Rightarrow\:\alpha^{\frac{\mathrm{n}^{\mathrm{2}} }{\mathrm{k}}} \left(\:\alpha^{\frac{\mathrm{m}^{\mathrm{2}} }{\mathrm{k}}\:−\:\frac{\mathrm{n}^{\mathrm{2}} }{\mathrm{k}}} −\:\mathrm{1}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\Rightarrow\:\alpha^{\frac{\mathrm{n}^{\mathrm{2}} }{\mathrm{k}}} =\:\mathrm{0}\:\vee\:\alpha^{\frac{\mathrm{m}^{\mathrm{2}} −\:\mathrm{n}^{\mathrm{2}} }{\mathrm{k}}} =\mathrm{1} \\ $$$$\:\:\:\:\:\Rightarrow\:\alpha=\mathrm{0}\:\:\vee\:\alpha=^{\frac{\mathrm{m}^{\mathrm{2}} \:−\:\mathrm{n}^{\mathrm{2}} }{\mathrm{k}}} \sqrt{\:\mathrm{1}}\:\:\:\:\left(\alpha\:\mathrm{is}\:\left(\frac{\mathrm{m}^{\mathrm{2}} \:−\:\mathrm{n}^{\mathrm{2}} }{\mathrm{k}}\right)\mathrm{th}\:\mathrm{root}\:\mathrm{of}\:\mathrm{unity}\right) \\ $$$$\alpha=\mathrm{0}\:\Rightarrow\beta=\mathrm{0}\:\:\:\:\left[\:\mathrm{No}\:\mathrm{need}\:\mathrm{to}\:\mathrm{show}\:\mathrm{process}\:\right] \\ $$$$\:\:\:\:\therefore\:\:\:\:\:\:\alpha\:\mathrm{is}\:\left(\frac{\mathrm{m}^{\mathrm{2}} \:−\:\mathrm{n}^{\mathrm{2}} }{\mathrm{k}}\right)\mathrm{th}\:\mathrm{root}\:\mathrm{of}\:\mathrm{unity}. \\ $$$$\mathrm{Similarly}\:\mathrm{it}\:\mathrm{can}\:\mathrm{be}\:\mathrm{shown}\:\mathrm{that}, \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\beta\:\:\mathrm{is}\:\mathrm{also}\:\:\left(\frac{\mathrm{m}^{\mathrm{2}} \:−\:\mathrm{n}^{\mathrm{2}} }{\mathrm{k}}\right)\mathrm{th}\:\mathrm{root}\:\mathrm{of}\:\mathrm{unity}. \\ $$$$\:\:\:\mathrm{nth}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{unity}\:\mathrm{are}\:\mathrm{given}\:\mathrm{by}:\: \\ $$$$\:\:\:\:\:\:\:\:\left(\:\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{n}}\:+\imath\:\mathrm{sin}\:\frac{\mathrm{2}\pi}{\mathrm{n}}\:\:\right)^{\mathrm{j}} \:\:\:\:\:\mathrm{j}=\mathrm{0},\mathrm{1},\mathrm{2},….,\mathrm{n}−\mathrm{1} \\ $$$$\mathrm{Hence}, \\ $$$$\:\:\:\:\:\:\:\left(\frac{\mathrm{m}^{\mathrm{2}} \:−\:\mathrm{n}^{\mathrm{2}} }{\mathrm{k}}\right)\:{th}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{unity}\:\mathrm{will}\:\mathrm{be}: \\ $$$$\:\:\:\:\:\left(\:\mathrm{cos}\:\frac{\mathrm{2}\pi\mathrm{k}}{\mathrm{m}^{\mathrm{2}} −\mathrm{n}^{\mathrm{2}} }\:+\imath\:\mathrm{sin}\:\frac{\mathrm{2}\pi\mathrm{k}}{\mathrm{m}^{\mathrm{2}} −\mathrm{n}^{\mathrm{2}} }\:\right)^{\mathrm{j}} \:\:\:\:\:\:\:\mathrm{j}=\mathrm{0},\mathrm{1},\mathrm{2},…\left(.\frac{\mathrm{m}^{\mathrm{2}} \:−\:\mathrm{n}^{\mathrm{2}} }{\mathrm{k}}\:−\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\mathrm{Let}\:\:\mathrm{cos}\:\frac{\mathrm{2}\pi\mathrm{k}}{\mathrm{m}^{\mathrm{2}} −\mathrm{n}^{\mathrm{2}} }\:+\imath\:\mathrm{sin}\:\frac{\mathrm{2}\pi\mathrm{k}}{\mathrm{m}^{\mathrm{2}} −\mathrm{n}^{\mathrm{2}} }\:\:\:\:=\omega \\ $$$$\left(\frac{\mathrm{m}^{\mathrm{2}} \:−\:\mathrm{n}^{\mathrm{2}} }{\mathrm{k}}\right)\:{th}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{unity}=\mathrm{1},\omega,\omega^{\mathrm{2}} ,……,\omega^{\frac{{m}^{\mathrm{2}} −\:\mathrm{n}^{\mathrm{2}} −\mathrm{k}}{\mathrm{k}}} \\ $$$$\left[\:\mathrm{Let}\:\frac{\mathrm{m}^{\mathrm{2}} −\mathrm{n}^{\mathrm{2}} }{\mathrm{k}}\:=\:\mathrm{N}\:\right] \\ $$$$\mathrm{m}{th}\:\mathrm{power}\:\mathrm{of}\:\:\:\:\backsim\:\:\:=\mathrm{1},\:\omega^{\:\mathrm{m}\left(\mathrm{mod}\:\mathrm{N}\right)} ,\omega^{\:\mathrm{2m}\left(\mathrm{mod}\:\mathrm{N}\right)} ,…\omega^{\:\mathrm{m}\left(\mathrm{N}−\mathrm{1}\right)\left(\mathrm{mod}\:\mathrm{N}\right)} \\ $$$$\mathrm{n}{th}\:\mathrm{power}\:\mathrm{of}\:\:\:\:\:\backsim\:\:\:\:=\mathrm{1},\:\omega^{\:\mathrm{n}\left(\mathrm{mod}\:\mathrm{N}\right)} ,\omega^{\:\mathrm{2n}\left(\mathrm{mod}\:\mathrm{N}\right)} ,…\omega^{\:\mathrm{n}\left(\mathrm{N}−\mathrm{1}\right)\left(\mathrm{mod}\:\mathrm{N}\right)} \\ $$$$\mathrm{Let}\:\:\mathrm{j}_{\mathrm{1}} \:,\:\mathrm{j}_{\mathrm{2}} =\mathrm{0},\mathrm{1},\mathrm{2},…\left(.\frac{\mathrm{m}^{\mathrm{2}} \:−\:\mathrm{n}^{\mathrm{2}} }{\mathrm{k}}\:−\mathrm{1}\right) \\ $$$$\mathrm{Let}\:\alpha\:=\:\omega^{\:{j}_{\mathrm{1}} } \:\:\mathrm{and}\:\beta\:=\:\:\omega^{\:\mathrm{j}_{\mathrm{2}} } \:\:\mathrm{are}\:\mathrm{two}\:\mathrm{N}{th}\:\mathrm{roots}\:\mathrm{such}\:\mathrm{that} \\ $$$$\:\:\alpha^{\mathrm{m}} =\beta^{\:\mathrm{n}} \Rightarrow\:\:\:\omega^{\:\mathrm{mj}_{\mathrm{1}} \left(\mathrm{mod}\:\mathrm{N}\right)} =\omega^{\:\mathrm{nj}_{\mathrm{2}} \left(\mathrm{mod}\:\mathrm{N}\right)} \Rightarrow\mathrm{mj}_{\mathrm{1}} \left(\mathrm{mod}\:\mathrm{N}\right)=\mathrm{nj}_{\mathrm{2}} \left(\mathrm{mod}\:\mathrm{N}\right) \\ $$$$\:\:\:\alpha^{\mathrm{n}} =\beta^{\:\mathrm{m}} \:\Rightarrow\:\:\:\omega^{\:\mathrm{nj}_{\mathrm{1}} \left(\mathrm{mod}\:\mathrm{N}\right)} =\omega^{\:\mathrm{mj}_{\mathrm{2}} \left(\mathrm{mod}\:\mathrm{N}\right)} \Rightarrow\mathrm{nj}_{\mathrm{1}} \left(\mathrm{mod}\:\mathrm{N}\right)=\mathrm{mj}_{\mathrm{2}} \left(\mathrm{mod}\:\mathrm{N}\right) \\ $$$$\mathrm{Therefore}\: \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$$\mathrm{For}\:\:\:\:\:\:\:\:\:\:\:\mathrm{mj}_{\mathrm{1}} \left(\mathrm{mod}\:\frac{\mathrm{m}^{\mathrm{2}} −\mathrm{n}^{\mathrm{2}} }{\mathrm{k}}\:\right)=\mathrm{nj}_{\mathrm{2}} \left(\mathrm{mod}\:\frac{\mathrm{m}^{\mathrm{2}} −\mathrm{n}^{\mathrm{2}} }{\mathrm{k}}\:\right)\: \\ $$$$\:\mathrm{and}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{nj}_{\mathrm{1}} \left(\mathrm{mod}\:\frac{\mathrm{m}^{\mathrm{2}} −\mathrm{n}^{\mathrm{2}} }{\mathrm{k}}\:\right)=\mathrm{mj}_{\mathrm{2}} \left(\mathrm{mod}\:\frac{\mathrm{m}^{\mathrm{2}} −\mathrm{n}^{\mathrm{2}} }{\mathrm{k}}\:\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\:\alpha,\:\beta\right)=\left(\omega^{\mathrm{j}_{\mathrm{1}} } ,\:\omega^{\mathrm{j}_{\mathrm{2}} } \right)=\left(\omega^{\mathrm{j}_{\mathrm{2}} } \:,\:\omega^{\mathrm{j}_{\mathrm{1}} } \right) \\ $$$$\:\mathrm{where}\:\:\omega\:\:\mathrm{is}\:\:\left(\frac{\mathrm{m}^{\mathrm{2}} \:−\:\mathrm{n}^{\mathrm{2}} }{\mathrm{k}}\right)\:{th}\:\mathrm{root}\:\mathrm{of}\:\mathrm{unity}\left(\:\mathrm{with}\:\mathrm{m}\geqslant\mathrm{n}\right). \\ $$
Answered by Rasheed Soomro last updated on 17/Aug/15

$$\boldsymbol{\mathrm{Formula}}\:\boldsymbol{\mathrm{for}}\:\boldsymbol{\mathrm{number}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{pairs}}\:\left(\boldsymbol{\alpha},\boldsymbol{\beta}\right)\:\boldsymbol{\mathrm{fulfilling}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{conditions}} \\ $$$$\boldsymbol{\mathrm{given}}\:\boldsymbol{\mathrm{in}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{question}}. \\ $$$$\frac{\boldsymbol{\mathrm{m}}^{\mathrm{2}} −\boldsymbol{\mathrm{n}}^{\mathrm{2}} +\boldsymbol{\mathrm{k}}}{\boldsymbol{\mathrm{k}}} \\ $$$$\boldsymbol{\mathrm{S}}\mathrm{ince}\:\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\:\:\left(\frac{\mathrm{m}^{\mathrm{2}} −\mathrm{n}^{\mathrm{2}} }{\mathrm{k}}\right){th}\:\mathrm{roots}\:\mathrm{is}\:\frac{\mathrm{m}^{\mathrm{2}} −\mathrm{n}^{\mathrm{2}} }{\mathrm{k}} \\ $$$$\mathrm{and}\:\mathrm{any}\:\mathrm{one}\:\mathrm{of}\:\mathrm{them}\:\mathrm{may}\:\mathrm{be}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\alpha\:\mathrm{and}\:\mathrm{to}\:\mathrm{every}\:\alpha\:\mathrm{one} \\ $$$$\mathrm{value}\:\mathrm{of}\:\beta\:\:\mathrm{is}\:\mathrm{attached}. \\ $$$$\mathrm{Hence}\:\mathrm{number}\:\mathrm{of}\:\left(\alpha,\beta\right)\:\mathrm{pairs}\:\mathrm{is}\:\:\frac{\mathrm{m}^{\mathrm{2}} −\mathrm{n}^{\mathrm{2}} }{\mathrm{k}}\:.\:\mathrm{But}\:\left(\mathrm{0},\mathrm{0}\right)\:\mathrm{also}\:\mathrm{satisfy}\:\mathrm{the} \\ $$$$\mathrm{conditions}\:\left(\mathrm{and}\:\mathrm{this}\:\mathrm{is}\:\mathrm{not}\:\mathrm{included}\:\mathrm{in}\:\mathrm{the}\:\mathrm{roots}\right)\: \\ $$$$\mathrm{So}\:\:\:\frac{\mathrm{m}^{\mathrm{2}} −\mathrm{n}^{\mathrm{2}} }{\mathrm{k}}+\mathrm{1}=\frac{\boldsymbol{\mathrm{m}}^{\mathrm{2}} −\boldsymbol{\mathrm{n}}^{\mathrm{2}} +\boldsymbol{\mathrm{k}}}{\boldsymbol{\mathrm{k}}}\:.\mathrm{Remember}\:\mathrm{that}\:\mathrm{k}=\mathrm{gcd}\left(\mathrm{m},\mathrm{n}\right)\:\mathrm{and} \\ $$$$\mathrm{m}\geqslant\mathrm{n}. \\ $$
Commented by Rasheed Soomro last updated on 20/Aug/15

$$\boldsymbol{{Who}}\:\boldsymbol{{did}}\:\boldsymbol{{like}}?\:\boldsymbol{{Suppose}}\:\boldsymbol{{liking}}\:\boldsymbol{{by}}\:\boldsymbol{{abc}}\:\boldsymbol{{is}}\:\boldsymbol{{more}}\:\boldsymbol{{important}} \\ $$$$\boldsymbol{{for}}\:\boldsymbol{{me}}\:\boldsymbol{{then}}\:\boldsymbol{{I}}\:\boldsymbol{{would}}\:\boldsymbol{{like}}\:\boldsymbol{{to}}\:\boldsymbol{{know}}\:\boldsymbol{{about}}\:\boldsymbol{{liker}}'\boldsymbol{{s}}\:\:\boldsymbol{{ID}}. \\ $$$$\boldsymbol{{So}}\:\boldsymbol{{liking}}\:\boldsymbol{{should}}\:\boldsymbol{{be}}\:\boldsymbol{{recorded}}\:\boldsymbol{{with}}\:\boldsymbol{{ID}}. \\ $$$$\boldsymbol{\mathrm{PL}}\:\boldsymbol{\mathrm{demand}}\:\boldsymbol{\mathrm{for}}\:\boldsymbol{\mathrm{this}}. \\ $$$$ \\ $$$$\boldsymbol{{Of}}\:\boldsymbol{{course}}\:\boldsymbol{{Likers}}'\:\:\boldsymbol{{ID}}'\boldsymbol{{s}}\:\:\boldsymbol{{shouldn}}'\boldsymbol{{t}}\:\boldsymbol{{be}}\:\boldsymbol{{there}}\:\boldsymbol{{for}}\:\boldsymbol{{full}} \\ $$$$\boldsymbol{{time}}\:\boldsymbol{{but}}\:\boldsymbol{{when}}\:\boldsymbol{{we}}\:\boldsymbol{{click}}…….\boldsymbol{{We}}\:\boldsymbol{{must}}\:\boldsymbol{{know}},\:''\:\boldsymbol{{Who}} \\ $$$$\boldsymbol{{did}}\:\boldsymbol{{like}}?\:'' \\ $$
