find-dU-if-U-x-2-e-x-y-

Question Number 71729 by peter frank last updated on 19/Oct/19

f i n d d U i f U = x^{2} e^{\frac{x}{y}}

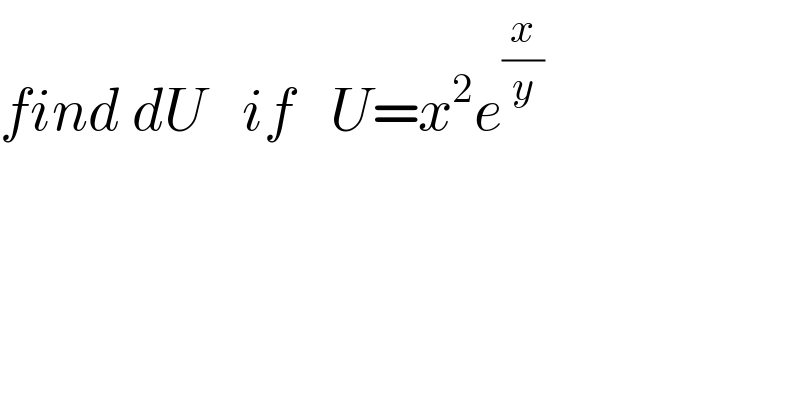
Commented by peter frank last updated on 19/Oct/19

t h a n k y o u

Commented by Prithwish sen last updated on 19/Oct/19

ylnu = 2 yln (x) + x

du = [2 {xe}^{\frac{x}{y}} dx + \frac{x^{2} e^{\frac{x}{y}}}{y} dx - \frac{x^{3}}{y^{2}} e^{\frac{x}{y}} dy] please check

Answered by mind is power last updated on 19/Oct/19

du = \frac{\partial u}{\partial x} dx + \frac{\partial u}{\partial y} dy

\frac{\partial}{\partial x} (x^{2} e^{\frac{x}{y}}) = (2 x + \frac{x^{2}}{y}) e^{\frac{x}{y}}

\frac{\partial}{\partial y} (x^{2} e^{\frac{x}{y}}) = - \frac{x^{3}}{y^{2}} e^{\frac{x}{y}}

\Rightarrow dU = (2 x + \frac{x^{2}}{y}) e^{\frac{x}{y}} dx - \frac{x^{3}}{y^{2}} e^{\frac{x}{y}} dy

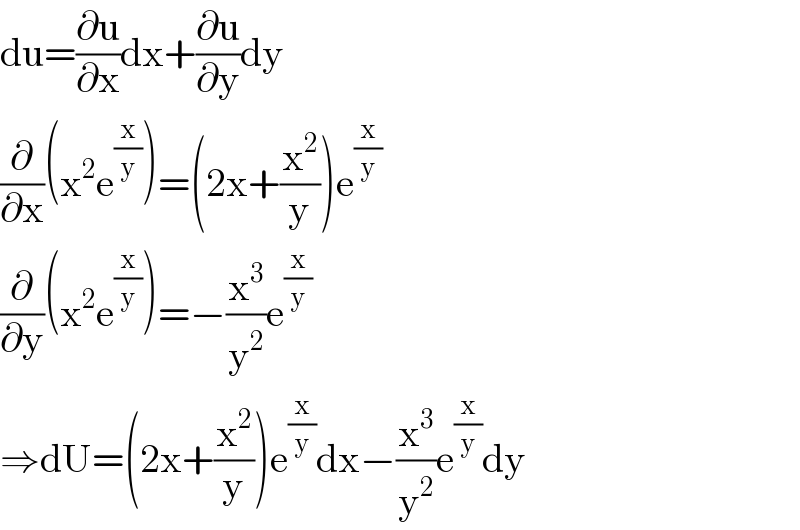
Commented by peter frank last updated on 19/Oct/19

t h a n k y o u