Menu Close

find-dx-x-3-x-2-4x-

Tinku Tara 0 Comments
Pin




Question Number 66308 by mathmax by abdo last updated on 12/Aug/19
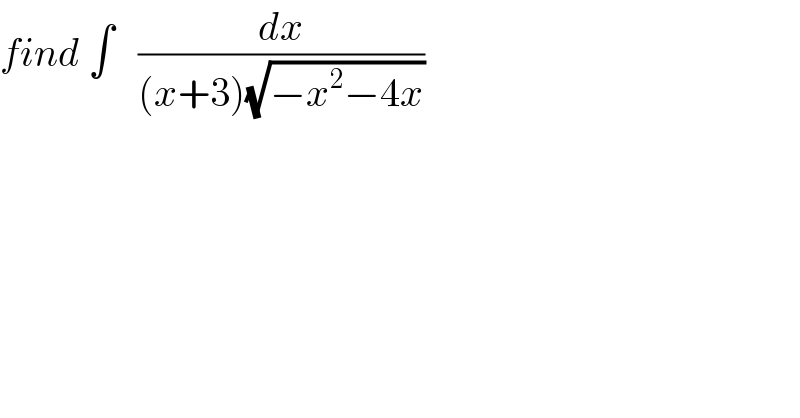
find ∫ (dx/((x+3)(√(−x^2 −4x))))
$${find}\:\int\:\:\:\frac{{dx}}{\left({x}+\mathrm{3}\right)\sqrt{−{x}^{\mathrm{2}} −\mathrm{4}{x}}} \\ $$
Commented by prof Abdo imad last updated on 16/Aug/19
let A =∫ (dx/((x+3)(√(−x^2 −4x)))) we have −x^2 −4x=−(x^2 +4x+4−4)=4−(x+2)^2 we use the changement x+2=2sint ⇒ A =∫ ((2cost dt)/((2sint−2+3)2cost)) =∫ (dt/(2sint +1)) =_(tan((t/2))=u) ∫ (1/((2((2u)/(1+u^2 ))+1)))((2du)/(1+u^2 )) =∫ ((2du)/((4u +1+u^2 ))) =∫ ((2du)/(u^2 +4u +1)) u^2 +4u +1=0→Δ^′ =4−1=3 ⇒ u_1 =−2+(√3) and u_2 =−2−(√(3 ))⇒ A = ∫ ((2du)/((u−u_1 )(u−u_2 ))) =(1/( (√3))) ∫ ((1/(u−u_1 ))−(1/(u−u_2 )))du =(1/( (√3)))ln∣((u−u_1 )/(u−u_2 ))∣+C=(1/( (√3)))ln∣((tan((t/2))+2−(√3))/(tan((t/2))+2+(√3)))∣ +C but t =arcsin(((x+2)/2)) ⇒ A =(1/( (√3)))ln∣((tan((1/2)arcsin((x/2)+1)+2−(√3))/(tan((1/2)arcsin((x/2)+1))+2+(√3)))∣ +C
$${let}\:{A}\:=\int\:\frac{{dx}}{\left({x}+\mathrm{3}\right)\sqrt{−{x}^{\mathrm{2}} −\mathrm{4}{x}}}\:\:{we}\:{have} \\ $$$$−{x}^{\mathrm{2}} −\mathrm{4}{x}=−\left({x}^{\mathrm{2}} \:+\mathrm{4}{x}+\mathrm{4}−\mathrm{4}\right)=\mathrm{4}−\left({x}+\mathrm{2}\right)^{\mathrm{2}} \\ $$$${we}\:{use}\:{the}\:{changement}\:{x}+\mathrm{2}=\mathrm{2}{sint}\:\Rightarrow \\ $$$${A}\:=\int\:\:\:\frac{\mathrm{2}{cost}\:{dt}}{\left(\mathrm{2}{sint}−\mathrm{2}+\mathrm{3}\right)\mathrm{2}{cost}}\:=\int\:\:\:\frac{{dt}}{\mathrm{2}{sint}\:+\mathrm{1}} \\ $$$$=_{{tan}\left(\frac{{t}}{\mathrm{2}}\right)={u}} \:\:\:\:\:\:\int\:\:\:\:\:\frac{\mathrm{1}}{\left(\mathrm{2}\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }+\mathrm{1}\right)}\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$=\int\:\:\:\:\:\frac{\mathrm{2}{du}}{\left(\mathrm{4}{u}\:+\mathrm{1}+{u}^{\mathrm{2}} \right)}\:=\int\:\:\:\frac{\mathrm{2}{du}}{{u}^{\mathrm{2}} \:+\mathrm{4}{u}\:+\mathrm{1}} \\ $$$${u}^{\mathrm{2}} \:+\mathrm{4}{u}\:+\mathrm{1}=\mathrm{0}\rightarrow\Delta^{'} \:=\mathrm{4}−\mathrm{1}=\mathrm{3}\:\Rightarrow \\ $$$${u}_{\mathrm{1}} =−\mathrm{2}+\sqrt{\mathrm{3}}\:{and}\:{u}_{\mathrm{2}} =−\mathrm{2}−\sqrt{\mathrm{3}\:}\Rightarrow \\ $$$${A}\:\:=\:\int\:\:\frac{\mathrm{2}{du}}{\left({u}−{u}_{\mathrm{1}} \right)\left({u}−{u}_{\mathrm{2}} \right)}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:\int\:\left(\frac{\mathrm{1}}{{u}−{u}_{\mathrm{1}} }−\frac{\mathrm{1}}{{u}−{u}_{\mathrm{2}} }\right){du} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}{ln}\mid\frac{{u}−{u}_{\mathrm{1}} }{{u}−{u}_{\mathrm{2}} }\mid+{C}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}{ln}\mid\frac{{tan}\left(\frac{{t}}{\mathrm{2}}\right)+\mathrm{2}−\sqrt{\mathrm{3}}}{{tan}\left(\frac{{t}}{\mathrm{2}}\right)+\mathrm{2}+\sqrt{\mathrm{3}}}\mid\:+{C} \\ $$$${but}\:{t}\:={arcsin}\left(\frac{{x}+\mathrm{2}}{\mathrm{2}}\right)\:\Rightarrow \\ $$$${A}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}{ln}\mid\frac{{tan}\left(\frac{\mathrm{1}}{\mathrm{2}}{arcsin}\left(\frac{{x}}{\mathrm{2}}+\mathrm{1}\right)+\mathrm{2}−\sqrt{\mathrm{3}}\right.}{{tan}\left(\frac{\mathrm{1}}{\mathrm{2}}{arcsin}\left(\frac{{x}}{\mathrm{2}}+\mathrm{1}\right)\right)+\mathrm{2}+\sqrt{\mathrm{3}}}\mid\:+{C} \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *