Question Number 11545 by Nayon last updated on 28/Mar/17
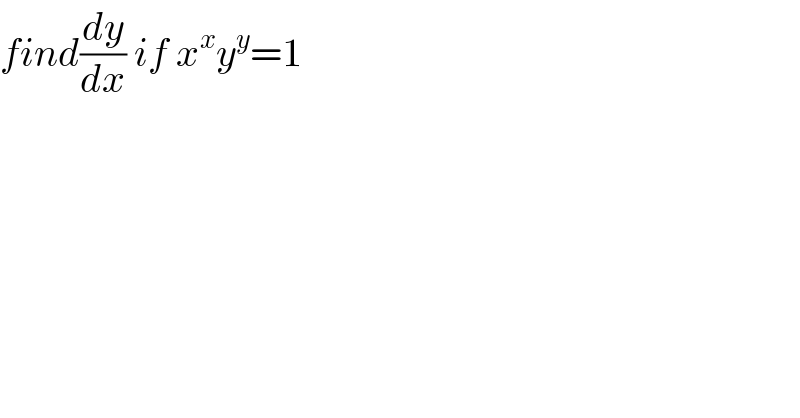
$${find}\frac{{dy}}{{dx}}\:{if}\:{x}^{{x}} {y}^{{y}} =\mathrm{1} \\ $$
Answered by Joel576 last updated on 28/Mar/17
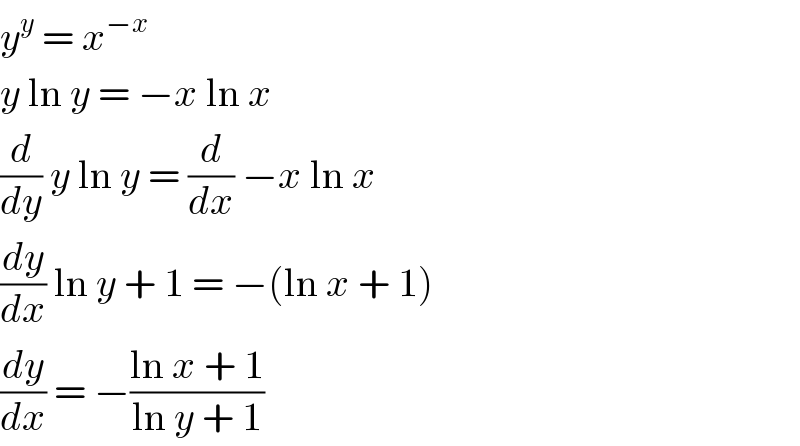
$${y}^{{y}} \:=\:{x}^{−{x}} \\ $$$${y}\:\mathrm{ln}\:{y}\:=\:−{x}\:\mathrm{ln}\:{x} \\ $$$$\frac{{d}}{{dy}}\:{y}\:\mathrm{ln}\:{y}\:=\:\frac{{d}}{{dx}}\:−{x}\:\mathrm{ln}\:{x} \\ $$$$\frac{{dy}}{{dx}}\:\mathrm{ln}\:{y}\:+\:\mathrm{1}\:=\:−\left(\mathrm{ln}\:{x}\:+\:\mathrm{1}\right) \\ $$$$\frac{{dy}}{{dx}}\:=\:−\frac{\mathrm{ln}\:{x}\:+\:\mathrm{1}}{\mathrm{ln}\:{y}\:+\:\mathrm{1}} \\ $$
Answered by ajfour last updated on 28/Mar/17
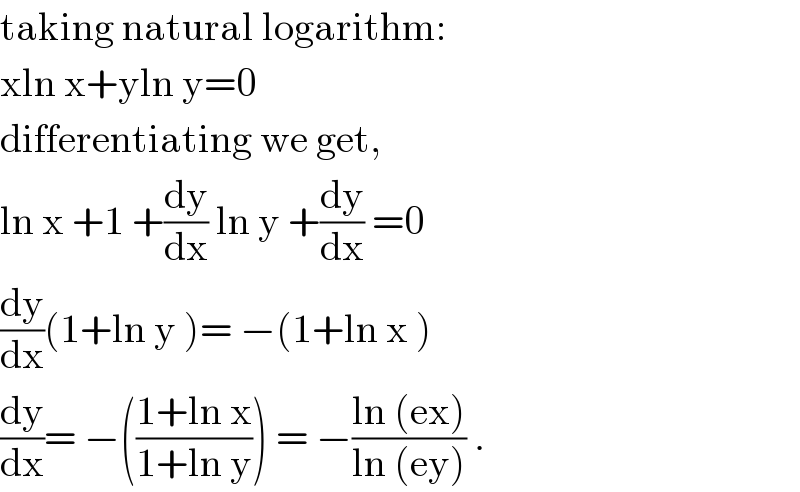
$$\mathrm{taking}\:\mathrm{natural}\:\mathrm{logarithm}: \\ $$$$\mathrm{xln}\:\mathrm{x}+\mathrm{yln}\:\mathrm{y}=\mathrm{0} \\ $$$$\mathrm{differentiating}\:\mathrm{we}\:\mathrm{get}, \\ $$$$\mathrm{ln}\:\mathrm{x}\:+\mathrm{1}\:+\frac{\mathrm{dy}}{\mathrm{dx}}\:\mathrm{ln}\:\mathrm{y}\:+\frac{\mathrm{dy}}{\mathrm{dx}}\:=\mathrm{0} \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}\left(\mathrm{1}+\mathrm{ln}\:\mathrm{y}\:\right)=\:−\left(\mathrm{1}+\mathrm{ln}\:\mathrm{x}\:\right) \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}=\:−\left(\frac{\mathrm{1}+\mathrm{ln}\:\mathrm{x}}{\mathrm{1}+\mathrm{ln}\:\mathrm{y}}\right)\:=\:−\frac{\mathrm{ln}\:\left(\mathrm{ex}\right)}{\mathrm{ln}\:\left(\mathrm{ey}\right)}\:. \\ $$
