Question Number 2484 by John_Haha last updated on 21/Nov/15
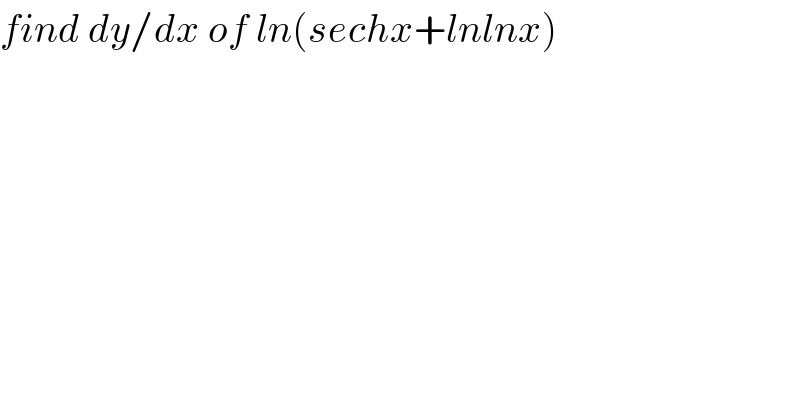
$${find}\:{dy}/{dx}\:{of}\:{ln}\left({sechx}+{lnlnx}\right) \\ $$
Answered by Filup last updated on 21/Nov/15
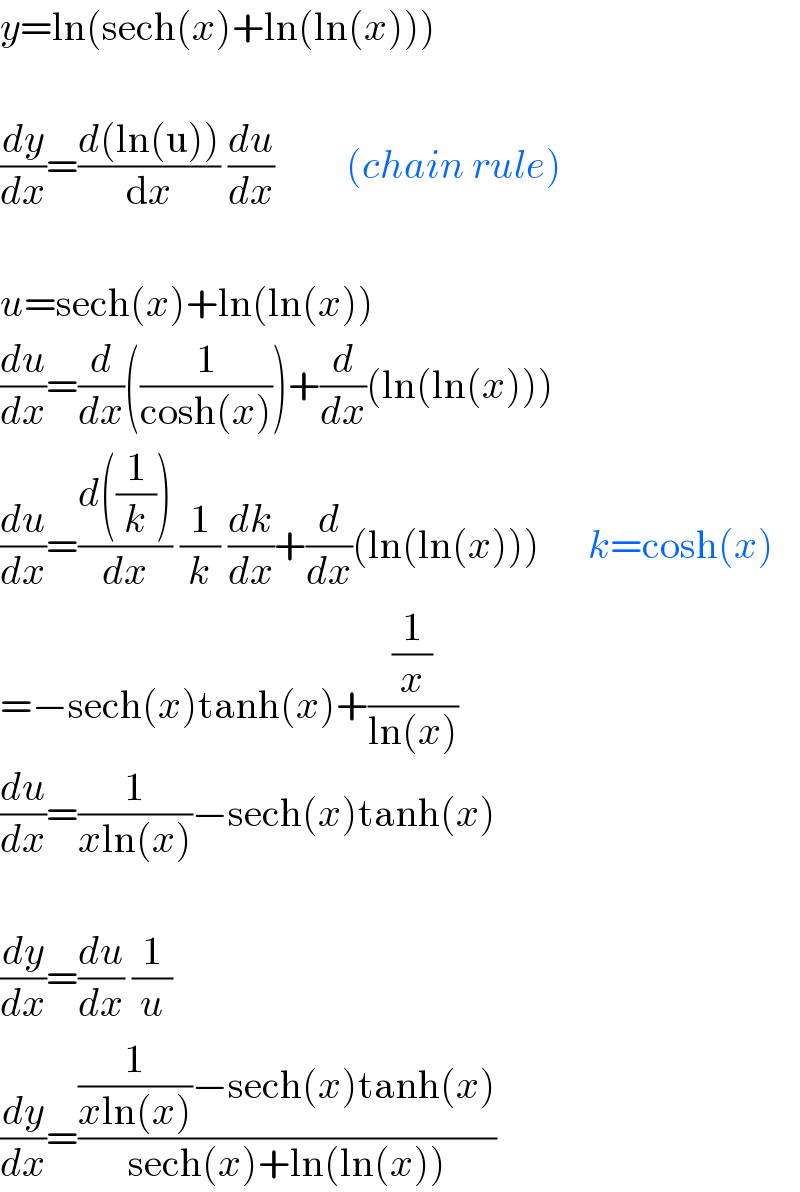
$${y}=\mathrm{ln}\left(\mathrm{sech}\left({x}\right)+\mathrm{ln}\left(\mathrm{ln}\left({x}\right)\right)\right) \\ $$$$ \\ $$$$\frac{{dy}}{{dx}}=\frac{{d}\left(\mathrm{ln}\left(\mathrm{u}\right)\right)}{\mathrm{d}{x}}\:\frac{{du}}{{dx}}\:\:\:\:\:\:\:\:\:\left({chain}\:{rule}\right) \\ $$$$ \\ $$$${u}=\mathrm{sech}\left({x}\right)+\mathrm{ln}\left(\mathrm{ln}\left({x}\right)\right) \\ $$$$\frac{{du}}{{dx}}=\frac{{d}}{{dx}}\left(\frac{\mathrm{1}}{\mathrm{cosh}\left({x}\right)}\right)+\frac{{d}}{{dx}}\left(\mathrm{ln}\left(\mathrm{ln}\left({x}\right)\right)\right) \\ $$$$\frac{{du}}{{dx}}=\frac{{d}\left(\frac{\mathrm{1}}{{k}}\right)}{{dx}}\:\frac{\mathrm{1}}{{k}}\:\frac{{dk}}{{dx}}+\frac{{d}}{{dx}}\left(\mathrm{ln}\left(\mathrm{ln}\left({x}\right)\right)\right)\:\:\:\:\:\:{k}=\mathrm{cosh}\left({x}\right) \\ $$$$=−\mathrm{sech}\left({x}\right)\mathrm{tanh}\left({x}\right)+\frac{\frac{\mathrm{1}}{{x}}}{\mathrm{ln}\left({x}\right)} \\ $$$$\frac{{du}}{{dx}}=\frac{\mathrm{1}}{{x}\mathrm{ln}\left({x}\right)}−\mathrm{sech}\left({x}\right)\mathrm{tanh}\left({x}\right) \\ $$$$ \\ $$$$\frac{{dy}}{{dx}}=\frac{{du}}{{dx}}\:\frac{\mathrm{1}}{{u}} \\ $$$$\frac{{dy}}{{dx}}=\frac{\frac{\mathrm{1}}{{x}\mathrm{ln}\left({x}\right)}−\mathrm{sech}\left({x}\right)\mathrm{tanh}\left({x}\right)}{\mathrm{sech}\left({x}\right)+\mathrm{ln}\left(\mathrm{ln}\left({x}\right)\right)} \\ $$
