Question Number 239 by 123456 last updated on 25/Jan/15
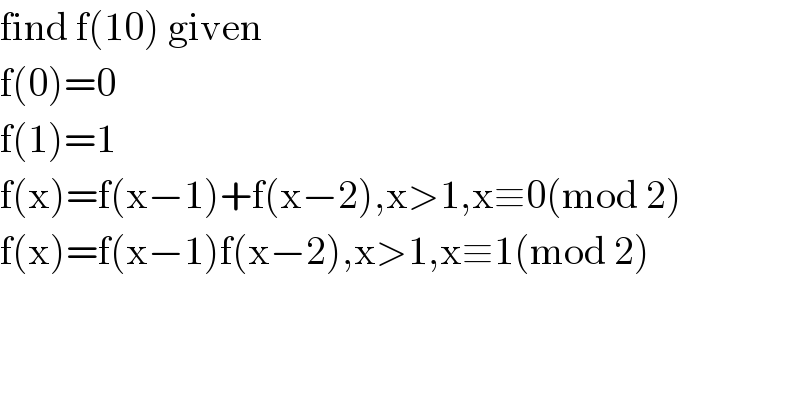
$$\mathrm{find}\:\mathrm{f}\left(\mathrm{10}\right)\:\mathrm{given} \\ $$$$\mathrm{f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\mathrm{f}\left(\mathrm{1}\right)=\mathrm{1} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{f}\left(\mathrm{x}−\mathrm{1}\right)+\mathrm{f}\left(\mathrm{x}−\mathrm{2}\right),\mathrm{x}>\mathrm{1},\mathrm{x}\equiv\mathrm{0}\left(\mathrm{mod}\:\mathrm{2}\right) \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{f}\left(\mathrm{x}−\mathrm{1}\right)\mathrm{f}\left(\mathrm{x}−\mathrm{2}\right),\mathrm{x}>\mathrm{1},\mathrm{x}\equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{2}\right) \\ $$
Answered by prakash jain last updated on 17/Dec/14

$$\mathrm{f}\left(\mathrm{2}\right)=\mathrm{f}\left(\mathrm{1}\right)+\mathrm{f}\left(\mathrm{0}\right)=\mathrm{1} \\ $$$$\mathrm{f}\left(\mathrm{3}\right)=\mathrm{f}\left(\mathrm{2}\right)\mathrm{f}\left(\mathrm{1}\right)=\mathrm{1} \\ $$$$\mathrm{f}\left(\mathrm{4}\right)=\mathrm{f}\left(\mathrm{3}\right)+\mathrm{f}\left(\mathrm{2}\right)=\mathrm{2} \\ $$$$\mathrm{f}\left(\mathrm{5}\right)=\mathrm{f}\left(\mathrm{4}\right)\mathrm{f}\left(\mathrm{3}\right)=\mathrm{2} \\ $$$$\mathrm{All}\:\mathrm{further}\:\mathrm{values}\:\mathrm{will}\:\mathrm{be}\:\mathrm{multiple}\:\mathrm{of}\:\mathrm{2} \\ $$$$\mathrm{so}\:\:\mathrm{f}\left(\mathrm{10}\right)\equiv\mathrm{0}\left(\mathrm{mod}\:\mathrm{2}\right) \\ $$$$\mathrm{f}\left(\mathrm{6}\right)=\mathrm{f}\left(\mathrm{5}\right)+\mathrm{f}\left(\mathrm{4}\right)=\mathrm{4} \\ $$$$\mathrm{f}\left(\mathrm{7}\right)=\mathrm{f}\left(\mathrm{6}\right)\mathrm{f}\left(\mathrm{5}\right)=\mathrm{8} \\ $$$$\mathrm{f}\left(\mathrm{8}\right)=\mathrm{f}\left(\mathrm{7}\right)+\mathrm{f}\left(\mathrm{6}\right)=\mathrm{12} \\ $$$$\mathrm{f}\left(\mathrm{9}\right)=\mathrm{f}\left(\mathrm{8}\right)\mathrm{f}\left(\mathrm{7}\right)=\mathrm{96} \\ $$$$\mathrm{f}\left(\mathrm{10}\right)=\mathrm{f}\left(\mathrm{9}\right)+\mathrm{f}\left(\mathrm{8}\right)=\mathrm{108} \\ $$
