Menu Close

Find-Find-K-0-pi-2-tan-d-

Tinku Tara 0 Comments
Pin




Question Number 67463 by ~ À ® @ 237 ~ last updated on 27/Aug/19
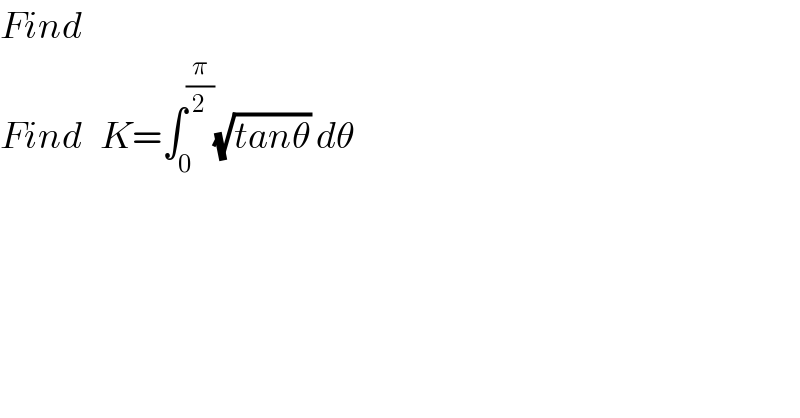
Find Find K=∫_0 ^(π/2) (√(tanθ)) dθ
$${Find} \\ $$$${Find}\:\:\:{K}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{{tan}\theta}\:{d}\theta\: \\ $$
Commented by ~ À ® @ 237 ~ last updated on 27/Aug/19
Using B(x,y)=2∫_0_ ^(π/2) (sinθ)^(2x−1) (cosθ)^(2y−1) dθ=((Γ(x)Γ(y))/(Γ(x+y))) 2K= 2∫_0 ^(π/2) (sinθ)^(1/2) (cosθ)^((−1)/2) dθ=2∫_0 ^(π/2) (sinθ)^(2((3/4))−1) (cosθ)^(2((1/4))−1) dθ = B((3/4),(1/4))=((Γ((3/4))Γ((1/4)))/(Γ(1)))=(π/(sin(((3π)/4))))=π(√(2 )) using complements formulas Γ(x)Γ(1−x)=(π/(sin(πx))) So K=(π/( (√2) ))
$$ \\ $$$${Using}\:{B}\left({x},{y}\right)=\mathrm{2}\int_{\mathrm{0}_{} } ^{\frac{\pi}{\mathrm{2}}} \left({sin}\theta\right)^{\mathrm{2}{x}−\mathrm{1}} \left({cos}\theta\right)^{\mathrm{2}{y}−\mathrm{1}} {d}\theta=\frac{\Gamma\left({x}\right)\Gamma\left({y}\right)}{\Gamma\left({x}+{y}\right)}\: \\ $$$$\mathrm{2}{K}=\:\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({sin}\theta\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \left({cos}\theta\right)^{\frac{−\mathrm{1}}{\mathrm{2}}} {d}\theta=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({sin}\theta\right)^{\mathrm{2}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)−\mathrm{1}} \left({cos}\theta\right)^{\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)−\mathrm{1}} {d}\theta \\ $$$$\:\:\:\:\:\:=\:{B}\left(\frac{\mathrm{3}}{\mathrm{4}},\frac{\mathrm{1}}{\mathrm{4}}\right)=\frac{\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right)}{\Gamma\left(\mathrm{1}\right)}=\frac{\pi}{{sin}\left(\frac{\mathrm{3}\pi}{\mathrm{4}}\right)}=\pi\sqrt{\mathrm{2}\:}\:\:\:\:\:\:{using}\:\:{complements}\:{formulas}\:\Gamma\left({x}\right)\Gamma\left(\mathrm{1}−{x}\right)=\frac{\pi}{{sin}\left(\pi{x}\right)}\: \\ $$$${So}\:\:{K}=\frac{\pi}{\:\sqrt{\mathrm{2}}\:} \\ $$
Commented by mathmax by abdo last updated on 27/Aug/19
let A =∫_0 ^(π/2) (√(tanθ))dθ cha7gement (√(tanθ))=t give tanθ =t^2 ⇒ θ =arctan(t^2 ) ⇒ A =∫_0 ^∞ ((t 2t)/(1+t^4 ))dt =2 ∫_0 ^∞ (t^2 /(1+t^4 ))dt changement t =x^(1/4) give A =2 ∫_0 ^∞ (x^(1/2) /(1+x))×(1/4)x^((1/4)−1) dx =(1/2) ∫_0 ^∞ (x^((1/2)+(1/4)−1) /(1+x))dx =(1/2)∫_0 ^∞ (x^((3/4)−1) /(1+x))dx =(1/2)×(π/(sin(((3π)/4)))) =(π/(2×((√2)/2))) =(π/( (√2))) ⇒ ★ ∫_0 ^(π/2) (√(tanθ))dθ =(π/( (√2))) ★ i have used the result ∫_0 ^∞ (t^(a−1) /(1+t))dt =(π/(sin(πa))) if 0<a<1.
$${let}\:\:{A}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\sqrt{{tan}\theta}{d}\theta\:\:\:{cha}\mathrm{7}{gement}\:\sqrt{{tan}\theta}={t}\:{give}\:{tan}\theta\:={t}^{\mathrm{2}} \:\Rightarrow \\ $$$$\theta\:={arctan}\left({t}^{\mathrm{2}} \right)\:\Rightarrow\:{A}\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{t}\:\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{4}} }{dt} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{4}} }{dt}\:\:\:\:\:{changement}\:{t}\:={x}^{\frac{\mathrm{1}}{\mathrm{4}}} \:{give}\:{A}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{x}^{\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{1}+{x}}×\frac{\mathrm{1}}{\mathrm{4}}{x}^{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} {dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}^{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} }{\mathrm{1}+{x}}{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\frac{{x}^{\frac{\mathrm{3}}{\mathrm{4}}−\mathrm{1}} }{\mathrm{1}+{x}}{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\pi}{{sin}\left(\frac{\mathrm{3}\pi}{\mathrm{4}}\right)} \\ $$$$=\frac{\pi}{\mathrm{2}×\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}\:=\frac{\pi}{\:\sqrt{\mathrm{2}}}\:\Rightarrow\:\bigstar\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{{tan}\theta}{d}\theta\:=\frac{\pi}{\:\sqrt{\mathrm{2}}}\:\bigstar \\ $$$${i}\:{have}\:{used}\:{the}\:{result}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}^{{a}−\mathrm{1}} }{\mathrm{1}+{t}}{dt}\:=\frac{\pi}{{sin}\left(\pi{a}\right)}\:{if}\:\:\mathrm{0}<{a}<\mathrm{1}. \\ $$
Commented by ~ À ® @ 237 ~ last updated on 27/Aug/19
thanks sir
$${thanks}\:{sir}\: \\ $$
Answered by Kunal12588 last updated on 27/Aug/19
I=∫(√(tan x)) dx let (√(tan x))=t ⇒[(1/(2(√(tan x))))×(1+tan^2 x)]dx=dt ⇒dx=((2t)/(1+t^4 ))dt I=∫((2t^2 )/(1+t^4 )) dt=∫ ((1+(1/t^2 ))/(t^2 +(1/t^2 )))dt + ∫ ((1−(1/t^2 ))/(t^2 +(1/t^2 )))dt =∫((d(t−(1/t)))/((t−(1/t))^2 +((√2))^2 ))+∫((d(t+(1/t)))/((t+(1/t))^2 −((√2))^2 )) =(1/( (√2)))tan^(−1) (((t^2 −1)/(t(√2))))+(1/(2(√2)))log∣((t^2 −(√2)t+1)/(t^2 +(√2)t+1))∣+C =(1/( (√2)))tan^(−1) (((tan x−1)/( (√(2tan x)))))+(1/(2(√2)))log∣((tan x−(√(2tan x))+1)/(tan x+(√(2tan x))+1))∣+C ∫_0 ^(π/2) (√(tan x))dx=∫_0 ^∞ ((2t^2 )/(1+t^4 ))dt lim_(t→∞) {(1/( (√2)))tan^(−1) ((t/( (√2)))−(1/(t(√2))))+(1/(2(√2)))log∣((1−((√2)/t)+(1/t^2 ))/(1+((√2)/t)+(1/t^2 )))∣+C} =(π/(2(√2))) lim_(t→0) {(1/( (√2)))tan^(−1) (((t^2 −1)/(t(√2))))+(1/(2(√2)))log∣((t^2 −(√2)t+1)/(t^2 +(√2)t+1))∣+C} =−(π/(2(√2))) ∫_0 ^(π/2) (√(tan x))dx=(π/(2(√2)))+(π/(2(√2)))=(π/( (√2)))=((π(√2))/2)
$${I}=\int\sqrt{{tan}\:{x}}\:{dx} \\ $$$${let}\:\sqrt{{tan}\:{x}}={t} \\ $$$$\Rightarrow\left[\frac{\mathrm{1}}{\mathrm{2}\sqrt{{tan}\:{x}}}×\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)\right]{dx}={dt} \\ $$$$\Rightarrow{dx}=\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{4}} }{dt} \\ $$$${I}=\int\frac{\mathrm{2}{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{4}} }\:{dt}=\int\:\frac{\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}{{t}^{\mathrm{2}} +\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}{dt}\:+\:\int\:\frac{\mathrm{1}−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}{{t}^{\mathrm{2}} +\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}{dt} \\ $$$$=\int\frac{{d}\left({t}−\frac{\mathrm{1}}{{t}}\right)}{\left({t}−\frac{\mathrm{1}}{{t}}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }+\int\frac{{d}\left({t}+\frac{\mathrm{1}}{{t}}\right)}{\left({t}+\frac{\mathrm{1}}{{t}}\right)^{\mathrm{2}} −\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \left(\frac{{t}^{\mathrm{2}} −\mathrm{1}}{{t}\sqrt{\mathrm{2}}}\right)+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{log}\mid\frac{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}+\mathrm{1}}{{t}^{\mathrm{2}} +\sqrt{\mathrm{2}}{t}+\mathrm{1}}\mid+{C} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \left(\frac{{tan}\:{x}−\mathrm{1}}{\:\sqrt{\mathrm{2}{tan}\:{x}}}\right)+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{log}\mid\frac{{tan}\:{x}−\sqrt{\mathrm{2}{tan}\:{x}}+\mathrm{1}}{{tan}\:{x}+\sqrt{\mathrm{2}{tan}\:{x}}+\mathrm{1}}\mid+{C} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{{tan}\:{x}}{dx}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2}{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{4}} }{dt} \\ $$$$\underset{{t}\rightarrow\infty} {{lim}}\left\{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \left(\frac{{t}}{\:\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{{t}\sqrt{\mathrm{2}}}\right)+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{log}\mid\frac{\mathrm{1}−\frac{\sqrt{\mathrm{2}}}{{t}}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}{\mathrm{1}+\frac{\sqrt{\mathrm{2}}}{{t}}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}\mid+{C}\right\} \\ $$$$=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {{lim}}\left\{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \left(\frac{{t}^{\mathrm{2}} −\mathrm{1}}{{t}\sqrt{\mathrm{2}}}\right)+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{log}\mid\frac{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}+\mathrm{1}}{{t}^{\mathrm{2}} +\sqrt{\mathrm{2}}{t}+\mathrm{1}}\mid+{C}\right\} \\ $$$$=−\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{{tan}\:{x}}{dx}=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}}+\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}}=\frac{\pi}{\:\sqrt{\mathrm{2}}}=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$
Commented by ~ À ® @ 237 ~ last updated on 27/Aug/19
Thanks you sir
$${Thanks}\:{you}\:{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *