Menu Close

find-k-1-n-k-C-n-k-2-interms-of-n-

Tinku Tara 0 Comments
Pin




Question Number 72389 by mathmax by abdo last updated on 28/Oct/19
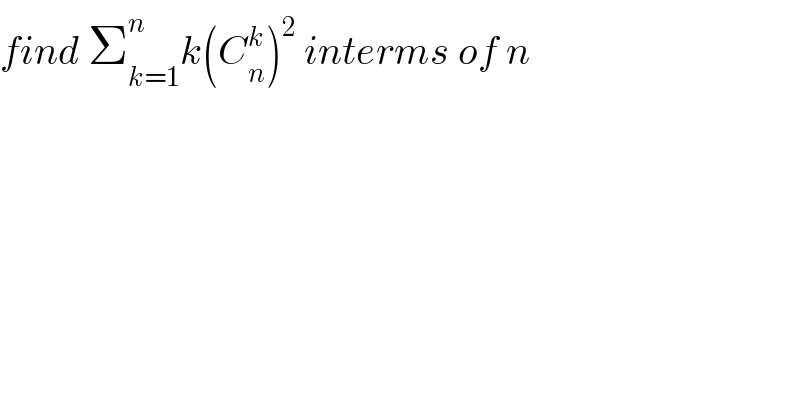
find Σ_(k=1) ^n k(C_n ^k )^2 interms of n
$${find}\:\sum_{{k}=\mathrm{1}} ^{{n}} {k}\left({C}_{{n}} ^{{k}} \right)^{\mathrm{2}} \:{interms}\:{of}\:{n} \\ $$
Answered by mind is power last updated on 28/Oct/19
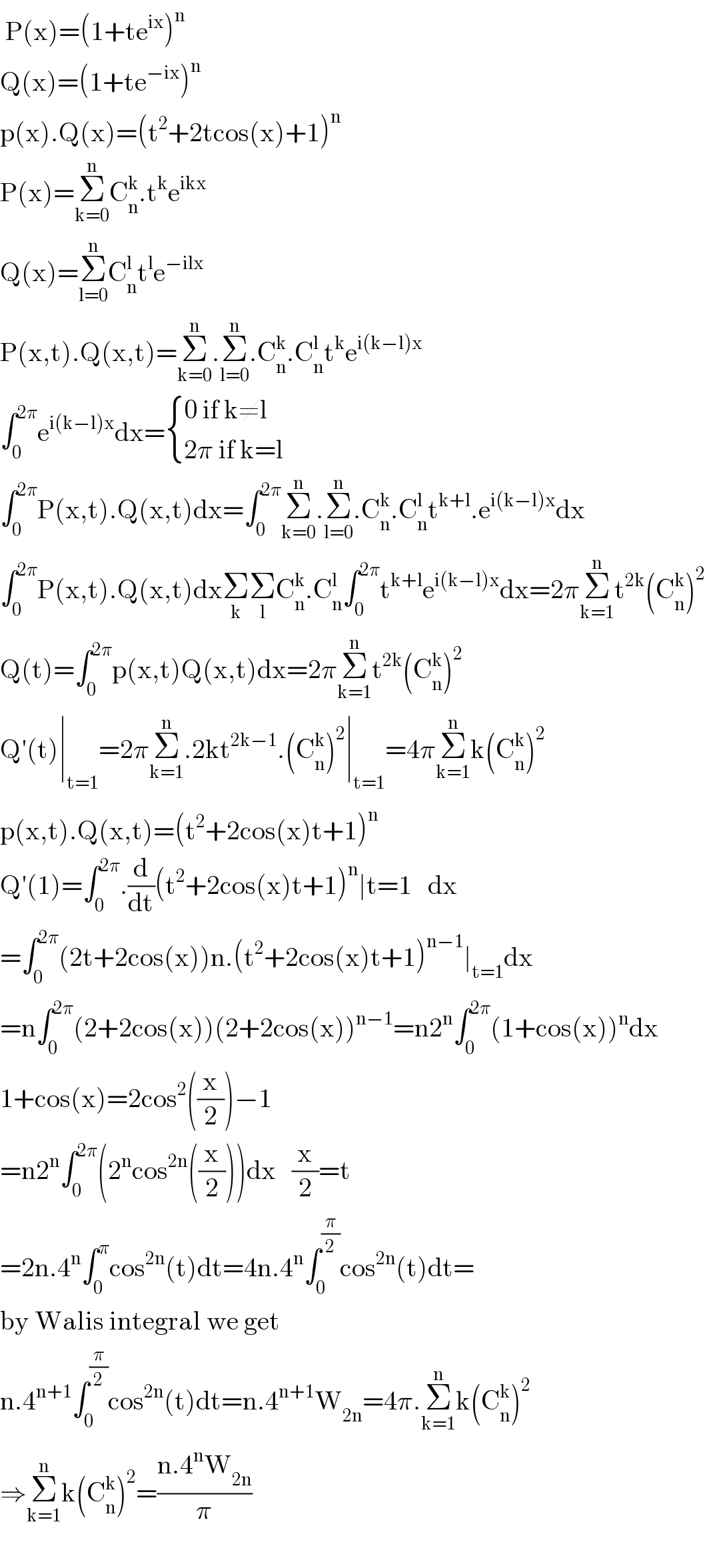
P(x)=(1+te^(ix) )^n Q(x)=(1+te^(−ix) )^n p(x).Q(x)=(t^2 +2tcos(x)+1)^n P(x)=Σ_(k=0) ^n C_n ^k .t^k e^(ikx) Q(x)=Σ_(l=0) ^n C_n ^l t^l e^(−ilx) P(x,t).Q(x,t)=Σ_(k=0) ^n .Σ_(l=0) ^n .C_n ^k .C_n ^l t^k e^(i(k−l)x) ∫_0 ^(2π) e^(i(k−l)x) dx= { ((0 if k≠l)),((2π if k=l)) :} ∫_0 ^(2π) P(x,t).Q(x,t)dx=∫_0 ^(2π) Σ_(k=0) ^n .Σ_(l=0) ^n .C_n ^k .C_n ^l t^(k+l) .e_ ^(i(k−l)x) dx ∫_0 ^(2π) P(x,t).Q(x,t)dxΣ_k Σ_l C_n ^k .C_n ^l ∫_0 ^(2π) t^(k+l) e^(i(k−l)x) dx=2πΣ_(k=1) ^n t^(2k) (C_n ^k )^2 Q(t)=∫_0 ^(2π) p(x,t)Q(x,t)dx=2πΣ_(k=1) ^n t^(2k) (C_n ^k )^2 Q′(t)∣_(t=1) =2πΣ_(k=1) ^n .2kt^(2k−1) .(C_n ^k )^2 ∣_(t=1) =4πΣ_(k=1) ^n k(C_n ^k )^2 p(x,t).Q(x,t)=(t^2 +2cos(x)t+1)^n Q′(1)=∫_0 ^(2π) .(d/dt)(t^2 +2cos(x)t+1)^n ∣t=1 dx =∫_0 ^(2π) (2t+2cos(x))n.(t^2 +2cos(x)t+1)^(n−1) ∣_(t=1) dx =n∫_0 ^(2π) (2+2cos(x))(2+2cos(x))^(n−1) =n2^n ∫_0 ^(2π) (1+cos(x))^n dx 1+cos(x)=2cos^2 ((x/2))−1 =n2^n ∫_0 ^(2π) (2^n cos^(2n) ((x/2)))dx (x/2)=t =2n.4^n ∫_0 ^π cos^(2n) (t)dt=4n.4^n ∫_0 ^(π/2) cos^(2n) (t)dt= by Walis integral we get n.4^(n+1) ∫_0 ^(π/2) cos^(2n) (t)dt=n.4^(n+1) W_(2n) =4π.Σ_(k=1) ^n k(C_n ^k )^2 ⇒Σ_(k=1) ^n k(C_n ^k )^2 =((n.4^n W_(2n) )/π)
$$\:\mathrm{P}\left(\mathrm{x}\right)=\left(\mathrm{1}+\mathrm{te}^{\mathrm{ix}} \right)^{\mathrm{n}} \\ $$$$\mathrm{Q}\left(\mathrm{x}\right)=\left(\mathrm{1}+\mathrm{te}^{−\mathrm{ix}} \right)^{\mathrm{n}} \\ $$$$\mathrm{p}\left(\mathrm{x}\right).\mathrm{Q}\left(\mathrm{x}\right)=\left(\mathrm{t}^{\mathrm{2}} +\mathrm{2tcos}\left(\mathrm{x}\right)+\mathrm{1}\right)^{\mathrm{n}} \\ $$$$\mathrm{P}\left(\mathrm{x}\right)=\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} .\mathrm{t}^{\mathrm{k}} \mathrm{e}^{\mathrm{ikx}} \\ $$$$\mathrm{Q}\left(\mathrm{x}\right)=\underset{\mathrm{l}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{C}_{\mathrm{n}} ^{\mathrm{l}} \mathrm{t}^{\mathrm{l}} \mathrm{e}^{−\mathrm{ilx}} \\ $$$$\mathrm{P}\left(\mathrm{x},\mathrm{t}\right).\mathrm{Q}\left(\mathrm{x},\mathrm{t}\right)=\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}.\underset{\mathrm{l}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}.\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} .\mathrm{C}_{\mathrm{n}} ^{\mathrm{l}} \mathrm{t}^{\mathrm{k}} \mathrm{e}^{\mathrm{i}\left(\mathrm{k}−\mathrm{l}\right)\mathrm{x}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \mathrm{e}^{\mathrm{i}\left(\mathrm{k}−\mathrm{l}\right)\mathrm{x}} \mathrm{dx}=\begin{cases}{\mathrm{0}\:\mathrm{if}\:\mathrm{k}\neq\mathrm{l}}\\{\mathrm{2}\pi\:\mathrm{if}\:\mathrm{k}=\mathrm{l}}\end{cases} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \mathrm{P}\left(\mathrm{x},\mathrm{t}\right).\mathrm{Q}\left(\mathrm{x},\mathrm{t}\right)\mathrm{dx}=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}.\underset{\mathrm{l}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}.\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} .\mathrm{C}_{\mathrm{n}} ^{\mathrm{l}} \mathrm{t}^{\mathrm{k}+\mathrm{l}} .\mathrm{e}_{} ^{\mathrm{i}\left(\mathrm{k}−\mathrm{l}\right)\mathrm{x}} \mathrm{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \mathrm{P}\left(\mathrm{x},\mathrm{t}\right).\mathrm{Q}\left(\mathrm{x},\mathrm{t}\right)\mathrm{dx}\underset{\mathrm{k}} {\sum}\underset{\mathrm{l}} {\sum}\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} .\mathrm{C}_{\mathrm{n}} ^{\mathrm{l}} \int_{\mathrm{0}} ^{\mathrm{2}\pi} \mathrm{t}^{\mathrm{k}+\mathrm{l}} \mathrm{e}^{\mathrm{i}\left(\mathrm{k}−\mathrm{l}\right)\mathrm{x}} \mathrm{dx}=\mathrm{2}\pi\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{t}^{\mathrm{2k}} \left(\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \right)^{\mathrm{2}} \\ $$$$\mathrm{Q}\left(\mathrm{t}\right)=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \mathrm{p}\left(\mathrm{x},\mathrm{t}\right)\mathrm{Q}\left(\mathrm{x},\mathrm{t}\right)\mathrm{dx}=\mathrm{2}\pi\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{t}^{\mathrm{2k}} \left(\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \right)^{\mathrm{2}} \\ $$$$\mathrm{Q}'\left(\mathrm{t}\right)\mid_{\mathrm{t}=\mathrm{1}} =\mathrm{2}\pi\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}.\mathrm{2kt}^{\mathrm{2k}−\mathrm{1}} .\left(\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \right)^{\mathrm{2}} \mid_{\mathrm{t}=\mathrm{1}} =\mathrm{4}\pi\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{k}\left(\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \right)^{\mathrm{2}} \\ $$$$\mathrm{p}\left(\mathrm{x},\mathrm{t}\right).\mathrm{Q}\left(\mathrm{x},\mathrm{t}\right)=\left(\mathrm{t}^{\mathrm{2}} +\mathrm{2cos}\left(\mathrm{x}\right)\mathrm{t}+\mathrm{1}\right)^{\mathrm{n}} \\ $$$$\mathrm{Q}'\left(\mathrm{1}\right)=\int_{\mathrm{0}} ^{\mathrm{2}\pi} .\frac{\mathrm{d}}{\mathrm{dt}}\left(\mathrm{t}^{\mathrm{2}} +\mathrm{2cos}\left(\mathrm{x}\right)\mathrm{t}+\mathrm{1}\right)^{\mathrm{n}} \mid\mathrm{t}=\mathrm{1}\:\:\:\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \left(\mathrm{2t}+\mathrm{2cos}\left(\mathrm{x}\right)\right)\mathrm{n}.\left(\mathrm{t}^{\mathrm{2}} +\mathrm{2cos}\left(\mathrm{x}\right)\mathrm{t}+\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \mid_{\mathrm{t}=\mathrm{1}} \mathrm{dx} \\ $$$$=\mathrm{n}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \left(\mathrm{2}+\mathrm{2cos}\left(\mathrm{x}\right)\right)\left(\mathrm{2}+\mathrm{2cos}\left(\mathrm{x}\right)\right)^{\mathrm{n}−\mathrm{1}} =\mathrm{n2}^{\mathrm{n}} \int_{\mathrm{0}} ^{\mathrm{2}\pi} \left(\mathrm{1}+\mathrm{cos}\left(\mathrm{x}\right)\right)^{\mathrm{n}} \mathrm{dx} \\ $$$$\mathrm{1}+\mathrm{cos}\left(\mathrm{x}\right)=\mathrm{2cos}^{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)−\mathrm{1} \\ $$$$=\mathrm{n2}^{\mathrm{n}} \int_{\mathrm{0}} ^{\mathrm{2}\pi} \left(\mathrm{2}^{\mathrm{n}} \mathrm{cos}^{\mathrm{2n}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)\mathrm{dx}\:\:\:\frac{\mathrm{x}}{\mathrm{2}}=\mathrm{t} \\ $$$$=\mathrm{2n}.\mathrm{4}^{\mathrm{n}} \int_{\mathrm{0}} ^{\pi} \mathrm{cos}^{\mathrm{2n}} \left(\mathrm{t}\right)\mathrm{dt}=\mathrm{4n}.\mathrm{4}^{\mathrm{n}} \int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}^{\mathrm{2n}} \left(\mathrm{t}\right)\mathrm{dt}= \\ $$$$\mathrm{by}\:\mathrm{Walis}\:\mathrm{integral}\:\mathrm{we}\:\mathrm{get}\:\: \\ $$$$\mathrm{n}.\mathrm{4}^{\mathrm{n}+\mathrm{1}} \int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}^{\mathrm{2n}} \left(\mathrm{t}\right)\mathrm{dt}=\mathrm{n}.\mathrm{4}^{\mathrm{n}+\mathrm{1}} \mathrm{W}_{\mathrm{2n}} =\mathrm{4}\pi.\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{k}\left(\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \right)^{\mathrm{2}} \\ $$$$\Rightarrow\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{k}\left(\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \right)^{\mathrm{2}} =\frac{\mathrm{n}.\mathrm{4}^{\mathrm{n}} \mathrm{W}_{\mathrm{2n}} }{\pi} \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 29/Oct/19
thank you sir.
$${thank}\:{you}\:{sir}. \\ $$
Commented by mind is power last updated on 29/Oct/19
y′re Welcom
$$\mathrm{y}'\mathrm{re}\:\mathrm{Welcom} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *