Question Number 135388 by Bird last updated on 12/Mar/21
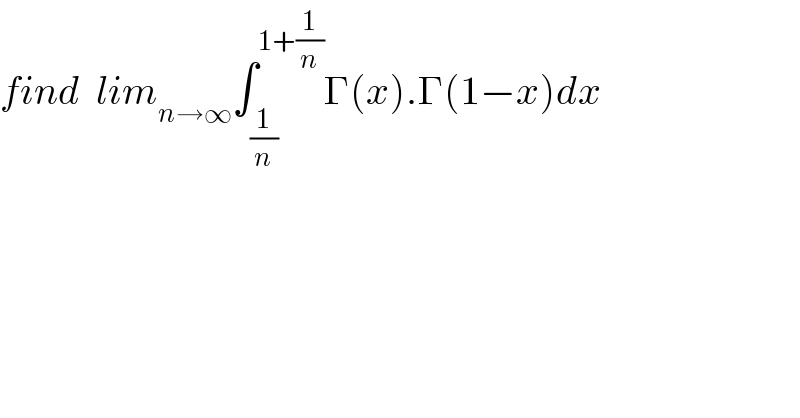
$${find}\:\:{lim}_{{n}\rightarrow\infty} \int_{\frac{\mathrm{1}}{{n}}} ^{\mathrm{1}+\frac{\mathrm{1}}{{n}}} \Gamma\left({x}\right).\Gamma\left(\mathrm{1}−{x}\right){dx} \\ $$
Answered by mathmax by abdo last updated on 15/Mar/21
![let U_n =∫_(1/n) ^(1+(1/n)) Γ(x).Γ(1−x)dx we have Γ(x).Γ(1−x)=(π/(sin(πx))) ⇒U_n =π∫_(1/n) ^(1+(1/n)) (dx/(sin(πx)))=_(πx=t) π ∫_(π/n) ^(π(1+(1/n))) (dt/(π sint)) =∫_(π/n) ^(π+(π/n)) (dt/(sint)) =_(tan((t/2))=z) ∫_(tan((π/(2n)))) ^(tan((π/2)+(π/(2n)))) ((2dz)/((1+z^2 ).((2z)/(1+z^2 )))) =[ln∣z∣]_(tan((π/(2n)))) ^(tan((π/2)+(π/(2n)))) =ln∣tan((π/2)+(π/(2n)))∣−ln∣tan((π/(2n)))∣ we have tan((π/2)+(π/(2n))) =((cos((π/(2n))))/(−sin((π/(2n))))) =−(1/(tan((π/(2n)))))∼−((2n)/π) ⇒ ∣tan((π/2)+(π/(2n)))∣∼ln(((2n)/π))→+∞ tan((π/(2n)))∼(π/(2n)) ⇒ln∣tan((π/(2n)))∣∼ln((π/(2n)))→−∞ ⇒lim_(n→+∞) U_n =+∞](https://www.tinkutara.com/question/Q135687.png)
$$\mathrm{let}\:\mathrm{U}_{\mathrm{n}} =\int_{\frac{\mathrm{1}}{\mathrm{n}}} ^{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}} \:\Gamma\left(\mathrm{x}\right).\Gamma\left(\mathrm{1}−\mathrm{x}\right)\mathrm{dx}\:\mathrm{we}\:\mathrm{have}\:\Gamma\left(\mathrm{x}\right).\Gamma\left(\mathrm{1}−\mathrm{x}\right)=\frac{\pi}{\mathrm{sin}\left(\pi\mathrm{x}\right)} \\ $$$$\Rightarrow\mathrm{U}_{\mathrm{n}} =\pi\int_{\frac{\mathrm{1}}{\mathrm{n}}} ^{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}} \:\frac{\mathrm{dx}}{\mathrm{sin}\left(\pi\mathrm{x}\right)}=_{\pi\mathrm{x}=\mathrm{t}} \:\:\pi\:\int_{\frac{\pi}{\mathrm{n}}} ^{\pi\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}\right)} \:\frac{\mathrm{dt}}{\pi\:\mathrm{sint}} \\ $$$$=\int_{\frac{\pi}{\mathrm{n}}} ^{\pi+\frac{\pi}{\mathrm{n}}} \:\frac{\mathrm{dt}}{\mathrm{sint}}\:=_{\mathrm{tan}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)=\mathrm{z}} \:\int_{\mathrm{tan}\left(\frac{\pi}{\mathrm{2n}}\right)} ^{\mathrm{tan}\left(\frac{\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{2n}}\right)} \:\frac{\mathrm{2dz}}{\left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \right).\frac{\mathrm{2z}}{\mathrm{1}+\mathrm{z}^{\mathrm{2}} }}\:=\left[\mathrm{ln}\mid\mathrm{z}\mid\right]_{\mathrm{tan}\left(\frac{\pi}{\mathrm{2n}}\right)} ^{\mathrm{tan}\left(\frac{\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{2n}}\right)} \\ $$$$=\mathrm{ln}\mid\mathrm{tan}\left(\frac{\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{2n}}\right)\mid−\mathrm{ln}\mid\mathrm{tan}\left(\frac{\pi}{\mathrm{2n}}\right)\mid\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{tan}\left(\frac{\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{2n}}\right)\:=\frac{\mathrm{cos}\left(\frac{\pi}{\mathrm{2n}}\right)}{−\mathrm{sin}\left(\frac{\pi}{\mathrm{2n}}\right)}\:=−\frac{\mathrm{1}}{\mathrm{tan}\left(\frac{\pi}{\mathrm{2n}}\right)}\sim−\frac{\mathrm{2n}}{\pi}\:\Rightarrow \\ $$$$\mid\mathrm{tan}\left(\frac{\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{2n}}\right)\mid\sim\mathrm{ln}\left(\frac{\mathrm{2n}}{\pi}\right)\rightarrow+\infty \\ $$$$\mathrm{tan}\left(\frac{\pi}{\mathrm{2n}}\right)\sim\frac{\pi}{\mathrm{2n}}\:\Rightarrow\mathrm{ln}\mid\mathrm{tan}\left(\frac{\pi}{\mathrm{2n}}\right)\mid\sim\mathrm{ln}\left(\frac{\pi}{\mathrm{2n}}\right)\rightarrow−\infty\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{U}_{\mathrm{n}} =+\infty \\ $$
